题目内容
 如图为反比例函数
如图为反比例函数 在第一象限的图象,点A为此图象上的一动点,过点A分别作AB⊥x轴和AC⊥y轴,垂足分别为B,C.则四边形OBAC周长的最小值为
在第一象限的图象,点A为此图象上的一动点,过点A分别作AB⊥x轴和AC⊥y轴,垂足分别为B,C.则四边形OBAC周长的最小值为
- A.4
- B.3
- C.2
- D.1
A
分析:首先表示出矩形边长,再利用长与宽的积为定值,且为正数,故考虑利用基本不等式即可解决.
解答:∵反比例函数 在第一象限的图象,点A为此图象上的一动点,过点A分别作
在第一象限的图象,点A为此图象上的一动点,过点A分别作
AB⊥x轴和AC⊥y轴,垂足分别为B,C.
∴四边形OBAC为矩形,
设宽BO=x,则AB= ,周长的一半表示为s,
,周长的一半表示为s,
则s=x+ ≥2
≥2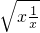 =2,
=2,
当且仅当x= ,即x=1时,取等号.
,即x=1时,取等号.
故函数s=x+ (x>0)的最小值为2.
(x>0)的最小值为2.
故2(x+ )=2×2=4,
)=2×2=4,
则四边形OBAC周长的最小值为4.
故选:A.
点评:此题考查了反比例函数的综合应用以及函数的最值问题,解答本题的关键是掌握不等式的基本性质,即a+b≥2 ,难度一般.
,难度一般.
分析:首先表示出矩形边长,再利用长与宽的积为定值,且为正数,故考虑利用基本不等式即可解决.
解答:∵反比例函数
 在第一象限的图象,点A为此图象上的一动点,过点A分别作
在第一象限的图象,点A为此图象上的一动点,过点A分别作AB⊥x轴和AC⊥y轴,垂足分别为B,C.
∴四边形OBAC为矩形,
设宽BO=x,则AB=
 ,周长的一半表示为s,
,周长的一半表示为s,则s=x+
 ≥2
≥2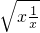 =2,
=2,当且仅当x=
 ,即x=1时,取等号.
,即x=1时,取等号.故函数s=x+
 (x>0)的最小值为2.
(x>0)的最小值为2.故2(x+
 )=2×2=4,
)=2×2=4,则四边形OBAC周长的最小值为4.
故选:A.
点评:此题考查了反比例函数的综合应用以及函数的最值问题,解答本题的关键是掌握不等式的基本性质,即a+b≥2
 ,难度一般.
,难度一般. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 作x轴的垂线,垂足为M,已知△AOM的面积为1,点B(-1,t)为反比例函数在第三象限图象上的点.
作x轴的垂线,垂足为M,已知△AOM的面积为1,点B(-1,t)为反比例函数在第三象限图象上的点.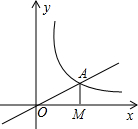 如图,正比例函数
如图,正比例函数 如图,正比例函数
如图,正比例函数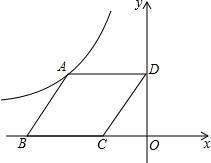 已知,如图,菱形ABCD的一边BC在x轴上,且C点坐标为(-1,0),D点坐标(0,
已知,如图,菱形ABCD的一边BC在x轴上,且C点坐标为(-1,0),D点坐标(0, 如图,正比例函数
如图,正比例函数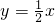 的图象与反比例函数
的图象与反比例函数 (k≠0)在第一象限的图象交于A点,过A点作x轴的垂线,垂足为M,已知△OAM的面积为1.
(k≠0)在第一象限的图象交于A点,过A点作x轴的垂线,垂足为M,已知△OAM的面积为1.