题目内容
解方程:(1)3x(x+2)=5(x+2)(2)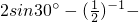 |-cot60°|+
|-cot60°|+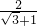 .
.
解:(1)3x(x+2)=5(x+2),
3x(x+2)-5(x+2)=0,
(x+2)(3x-5)=0,
∴x+2=0或3x-5=0,
x1=-2,x2= .
.
(2)原式=2× -2-
-2- +
+ -1
-1
=-2+ .
.
分析:(1)用因式分解法解方程;
(2)把特殊角的三角函数值代入进行计算.
点评:(1)解一元二次方程要选用适当的方法.(2)掌握负整数指数和绝对值的意义,记住特殊角的三角函数值.
3x(x+2)-5(x+2)=0,
(x+2)(3x-5)=0,
∴x+2=0或3x-5=0,
x1=-2,x2=
 .
.(2)原式=2×
 -2-
-2- +
+ -1
-1=-2+
 .
.分析:(1)用因式分解法解方程;
(2)把特殊角的三角函数值代入进行计算.
点评:(1)解一元二次方程要选用适当的方法.(2)掌握负整数指数和绝对值的意义,记住特殊角的三角函数值.

练习册系列答案
相关题目