Question

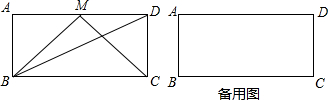
（2012•和平区二模）矩形ABCD中，点M是边AD上一点，连接BM、CM．
（1）如图，若AM=DM，∠BMC=90°，试判断线段BM与CM的数量关系，并说明理由；
（2）若AB=2

3

，AD=8，∠BMC=90°．①求线段AM的长；②若点N在边BC上，且∠AND=90°，则线段MN的长是

2

3

或2

7

．

Answer 1

分析：（1）根据矩形的性质得AD=CD，∠A=∠D=90°，则可根据“SAS”判断△ABM≌△DCM，所以BM=CM；
（2）①利用等角的余角相等得到∠ABM=∠CMD，于是可判断Rt△ABM∽Rt△DMC，所以

AB

MD

=

AM

DC

，设AM=x，则DM=8-x，则

2 3

8-x

=

x

2 3

，解得x₁=2，x₂=6，
②同理可得AN的长为2或6，讨论：当AM=2，AN=2，则MN=AB=2

3

；当AM=2，AN′=6（即N落在N′的位置），利用勾股定理可计算出MN′=2

7

，所以MN的长为2

3

或2

7

．

解答：解：（1）线段BM与CM的数量关系为相等．理由如下：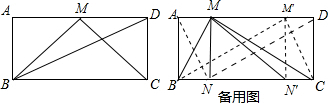
∵四边形ABCD为矩形，
∴AD=CD，∠A=∠D=90°，
在△ABM和△DCM中，

AD=DC ∠BAM=∠MDC AM=DM

，
∴△ABM≌△DCM（SAS），
∴BM=CM；

（2）①∵∠BMC=90°，
∴∠AMB+∠CMD=90°，
而∠AMB+∠ABM=90°，
∴∠ABM=∠CMD，
∴Rt△ABM∽Rt△DMC，
∴

AB

MD

=

AM

DC

，
∵AB=2

3

，AD=8，
∴DC=2

3

，
设AM=x，则DM=8-x，
∴

2 3

8-x

=

x

2 3

，
解得x₁=2，x₂=6，
∴AM的长为2或6；
②若点N在边BC上，且∠AND=90°，
同理可得AN的长为2或6，
如图，
当AM=2，AN=2，则MN=AB=2

3

，
当AM=2，AN′=6（即N落在N′的位置），则NN′=4，
∴MN′=

(2 3 )2+42

=2

7

，
∴MN的长为2

3

或2

7

．

点评：本题考查了相似三角形的判定与性质：有两组角对应相等的两个三角形相似；相似三角形的对应边的比相等，相似三角形面积的比等于相似比的平方．也考查了矩形的性质、三角形全等与相似的判定与性质．