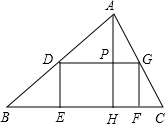
题目内容
 如图,E是矩形ABCD的边AD上一点,且BE=ED,P是对角线BD上任意一点,PF⊥BE,PG⊥AD,垂足分别为F、G.求证:PF+PG=AB.
如图,E是矩形ABCD的边AD上一点,且BE=ED,P是对角线BD上任意一点,PF⊥BE,PG⊥AD,垂足分别为F、G.求证:PF+PG=AB.分析:连接PE,把△BED分成△BEP和△DEP两个三角形,然后利用三角形的面积列式进行计算即可得证.
解答: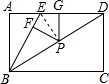 证明:连接PE,∵BE=ED,PF⊥BE,PG⊥AD,
证明:连接PE,∵BE=ED,PF⊥BE,PG⊥AD,
∴S△BDE=S△BEP+S△DEP
=
BE•PF+
ED•PG
=
ED•(PF+PG),
又∵四边形ABCD是矩形,
∴BA⊥AD,
∴S△BED=
ED•AB,
∴
ED•(PF+PG)=
ED•AB,
∴PF+PG=AB.
 证明:连接PE,∵BE=ED,PF⊥BE,PG⊥AD,
证明:连接PE,∵BE=ED,PF⊥BE,PG⊥AD,∴S△BDE=S△BEP+S△DEP
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
又∵四边形ABCD是矩形,
∴BA⊥AD,
∴S△BED=
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴PF+PG=AB.
点评:本题考查了矩形的性质,三角形的面积,作辅助线,利用三角形的面积的两种表示方法证明更简单.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

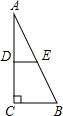 如图,在一张△ABC纸片中,∠C=90°,∠B=60°,DE是中位线,现把纸片沿中位线DE剪开,计划拼出以下四个图形:①邻边不等的矩形;②等腰梯形;③有两个角为锐角的菱形;④正方形.那么以上图形一定能被拼成的个数为( )
如图,在一张△ABC纸片中,∠C=90°,∠B=60°,DE是中位线,现把纸片沿中位线DE剪开,计划拼出以下四个图形:①邻边不等的矩形;②等腰梯形;③有两个角为锐角的菱形;④正方形.那么以上图形一定能被拼成的个数为( )