题目内容
已知:如图,在 ABCD中,点F在AB的延长线上,且BF=AB,连接FD,交BC于点E.
ABCD中,点F在AB的延长线上,且BF=AB,连接FD,交BC于点E.
(1)说明△DCE≌△FBE的理由;
(2)若EC=3,求AD的长.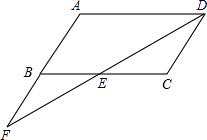
 ABCD中,点F在AB的延长线上,且BF=AB,连接FD,交BC于点E.
ABCD中,点F在AB的延长线上,且BF=AB,连接FD,交BC于点E.(1)说明△DCE≌△FBE的理由;
(2)若EC=3,求AD的长.

(1)证明见解析(2)6
(1)证明:∵四边形ABCD是平行四边形,∴AB=DC,AB∥DC。∴∠CDE=∠F。
又∵BF=AB,∴DC=FB。
在△DCE和△FBE中,∵∠CDE=∠F,∠CED=∠BEF, DC=FB,
∴△DCE≌△FBE(AAS)。
(2)解:∵△DCE≌△FBE,∴EB=EC。
∵EC=3,∴BC=2EB=6。
∵四边形ABCD是平行四边形,∴AD=BC。∴AD=6
(1)由四边形ABCD是平行四边形,根据平行四边形的对边平行且相等,即可得AB=DC,AB∥DC,继而可求得∠CDE=∠F,又由BF=AB,即可利用AAS,判定△DCE≌△FBE。
(2)由(1),可得BE=EC,即可求得BC的长,又由平行四边形的对边相等,即可求得AD的长
又∵BF=AB,∴DC=FB。
在△DCE和△FBE中,∵∠CDE=∠F,∠CED=∠BEF, DC=FB,
∴△DCE≌△FBE(AAS)。
(2)解:∵△DCE≌△FBE,∴EB=EC。
∵EC=3,∴BC=2EB=6。
∵四边形ABCD是平行四边形,∴AD=BC。∴AD=6
(1)由四边形ABCD是平行四边形,根据平行四边形的对边平行且相等,即可得AB=DC,AB∥DC,继而可求得∠CDE=∠F,又由BF=AB,即可利用AAS,判定△DCE≌△FBE。
(2)由(1),可得BE=EC,即可求得BC的长,又由平行四边形的对边相等,即可求得AD的长

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
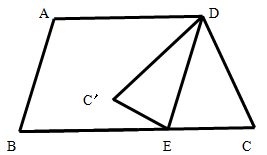
 中,
中, ,
, ,边
,边 绕
绕 旋转使得点
旋转使得点 落在射线
落在射线 上
上 处,那么
处,那么 的度数为 .
的度数为 .




