Question

【题目】，，为的角平分线.

（1）如图1，若，则______；若，则______；猜想：与的数量关系为______

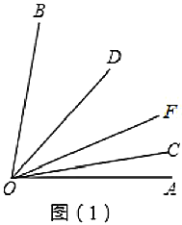
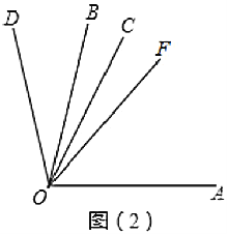
（2）当绕点按逆时针旋转至图2的位置时，（1）的数量关系是否仍然成立？请说明理由.

（3）如图3，在（2）的条件下，在中作射线，使，且，直接写出______.

Answer 1

【答案】（1），，；（2）见解析；（3）16°

【解析】

（1）由已知求出∠DOF=30°，由角平分线得出∠AOF=∠DOF=30°，得出∠AOD=60°，求出∠BOD=∠AOB-∠AOD=20°；若∠COF=m°，则∠DOF=40°-m°，由角平分线得出∠AOF=∠DOF=40°-m°，得出∠AOD=80°-2m°，得出∠BOD=∠AOB-∠AOD=2m°，即可得出结论；

（2）设，则，利用角平分线的性质即可得出，（1）的数量关系依然成立；

（3）设，则，得出，由角平分线得出，由∠AOB=80°得出方程，解方程求出，即可得出结果．

（1）∵，

∴∠FOD=∠COD-∠COF=40°-10°=30°

∵为的角平分线

∴∠AOD=2∠FOD=60°

∵，

∴∠BOD=∠AOB-∠AOD=80°-60°=20°

同理可得，∠BOD=，

∵∠COD=40°，∠COF=10°，

∴∠DOF=30°，

∵OF为∠AOD的角平分线．

∴∠AOF=∠DOF=30°，

∴∠AOD=60°，

∴∠BOD=∠AOB-∠AOD=20°；

∵∠COD=40°，∠COF=m°，

∴∠DOF=40°-m°，

∵OF为∠AOD的角平分线．

∴∠AOF=∠DOF=40°-m°，

∴∠AOD=80°-2m°，

∴∠BOD=∠AOB-∠AOD=2m°，

∴∠BOD=2∠COF；

通过上述两种求法，可得.

（2）∵，设，则．

∵为的角平分线，

∴

∵，

∴，

∴.（1）的数量关系依然成立．

（3）设，则，

∴，

∵为的平分线，

∴

∵，

∴，解得，

∴