题目内容
已知⊙O的弦AB=2a，圆心O到该弦的距离为b，则圆的周长为（ ）
| A、2πb2 | ||
| B、2πa2 | ||
C、2π
| ||
| D、2π（a+b）2 |
分析：根据垂径定理和勾股定理可将圆的半径求出，代入圆的周长公式C=2πR，即可求出．
解答：解：设⊙O的半径为R
∵弦AB=2a，圆心O到该弦的距离为b
∴R=
=
∴圆的周长C=2πR=2π
故选C．
∵弦AB=2a，圆心O到该弦的距离为b
∴R=
(
|
| a2+b2 |
∴圆的周长C=2πR=2π
| a2+b2 |
故选C．
点评：本题综合考查了垂径定理和勾股定理的性质和运用．
练习册系列答案
阅读快车系列答案
相关题目
如图，已知⊙O的弦AB、CD相交于点E， |
| AC |
|
| BD |
| A、60° | B、100° |
| C、80° | D、130° |
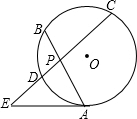如图，已知⊙O的弦AB、CD相交于点P，PA=4cm，PB=3cm，PC=6cm，EA切⊙O于点A，AE与CD的延长线交于点E，若AE=2| 5 |
| A、4cm | ||
| B、3cm | ||
| C、5cm | ||
D、
|
已知⊙O的弦AB、CD相交于点E，