题目内容
11.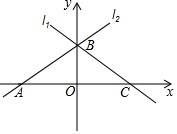 如图,直线l1与直线l2关于y轴对称,已知直线l1的函数表达式为y=-$\frac{4}{3}$x+b,点B 坐标为(0,3),则点A坐标为(-$\frac{9}{4}$,0).
如图,直线l1与直线l2关于y轴对称,已知直线l1的函数表达式为y=-$\frac{4}{3}$x+b,点B 坐标为(0,3),则点A坐标为(-$\frac{9}{4}$,0).
分析 先将点B 坐标(0,3)代入y=-$\frac{4}{3}$x+b,求出直线l1的解析式,再根据关于y轴对称的点纵坐标不变横坐标互为相反数求出直线l2的解析式,进而得出点A坐标.
解答 解:将点B 坐标(0,3)代入y=-$\frac{4}{3}$x+b,得b=3,
则直线l1的解析式为y=-$\frac{4}{3}$x+3,
∵直线l1与直线l2关于y轴对称,
∴直线l2的解析式为y=$\frac{4}{3}$x+3,
令y=0,得$\frac{4}{3}$x+3=0,解得x=-$\frac{9}{4}$,
∴点A坐标为(-$\frac{9}{4}$,0).
故答案为(-$\frac{9}{4}$,0).
点评 本题主要考查的是一次函数的图象与几何变换,熟知关于y轴对称的点的坐标特点是解答此题的关键.

练习册系列答案
相关题目
2.由表的对应值知,一元二次方程ax2+bx+c=0(a,b,c为常数,a≠0)的一个根的百分位上的数字是4.
| x | 3.23 | 3.24 | 3.25 | 3.26 |
| ax2+bx+c | -0.06 | -0.02 | 0.03 | 0.09 |
6.点(a-2,b+2)经过平移变换得到点(a,b),则这个平移变换是( )
| A. | 先向左平移2个单位长度,再向下平移2个单位长度 | |
| B. | 先向左平移2个单位长度,再向上平移2个单位长度 | |
| C. | 先向右平移2个单位长度,再向下平移2个单位长度 | |
| D. | 先向右平移2个单位长度,再向上平移2个单位长度 |
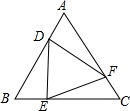 如图,等边△ABC中,点D,E,F分别同时从点A,B,C出发,以相同的速度在AB,BC,CA上运动,连结DE,EF,DF.
如图,等边△ABC中,点D,E,F分别同时从点A,B,C出发,以相同的速度在AB,BC,CA上运动,连结DE,EF,DF.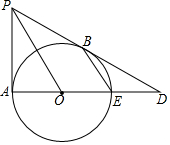 如图,PA,PB分别与⊙O相切于点A,B,延长PB交直径AE的延长线于点D.
如图,PA,PB分别与⊙O相切于点A,B,延长PB交直径AE的延长线于点D.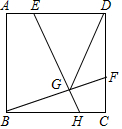 如图,正方形ABCD中,点E在边AD上,点F在边CD上,AE=CF,EH⊥BF于点G,连接DG.
如图,正方形ABCD中,点E在边AD上,点F在边CD上,AE=CF,EH⊥BF于点G,连接DG.