题目内容
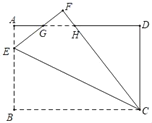
【题目】如图,![]() ,
,![]() ,点
,点![]() 在
在![]() 轴上,且
轴上,且![]() .
.
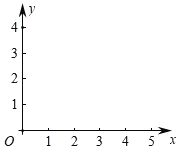
(1)求点![]() 的坐标,并画出
的坐标,并画出![]() ;
;
(2)求![]() 的面积;
的面积;
(3)在![]() 轴上是否存在点
轴上是否存在点![]() ,使以
,使以![]() 三点为顶点的三角形的面积为10?若存在,请直接写出点
三点为顶点的三角形的面积为10?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() 点的坐标为
点的坐标为![]() ,
,![]() ,画图见解析;(2) 6;(3)
,画图见解析;(2) 6;(3)![]() 点的坐标为
点的坐标为![]() 或
或![]()
【解析】
(1)分点B在点A的左边和右边两种情况解答;
(2)利用三角形的面积公式列式计算即可得解;
(3)利用三角形的面积公式列式求出点P到x轴的距离,然后分两种情况写出点P的坐标即可.
(1)点B在点A的右边时,-1+3=2,
点B在点A的左边时,-1-3=-4,
所以,B的坐标为(2,0)或(-4,0),
如图所示:
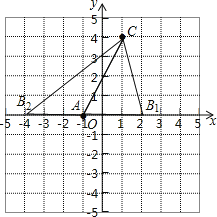
(2)△ABC的面积=![]() ×3×4=6;
×3×4=6;
(3)设点P到x轴的距离为h,
则![]() ×3h=10,
×3h=10,
解得h=![]() ,
,
点P在y轴正半轴时,P(0,![]() ),
),
点P在y轴负半轴时,P(0,-![]() ),
),
综上所述,点P的坐标为(0,![]() )或(0,-
)或(0,-![]() ).
).

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
【题目】[问题情境]
已知矩形的面积为一定值1,当该矩形的一组邻边分别为多少时,它的周长最小?最小值是多少?
[数学模型]
设该矩形的一边长为x,周长为L,则L与x的函数表达式为 .
[探索研究]
小彬借鉴以前研究函数的经验,先探索函数![]() 的图象性质.
的图象性质.
(1)结合问题情境,函数![]() 的自变量x的取值范围是 ,
的自变量x的取值范围是 ,
如表是y与x的几组对应值.
x | … |
|
|
| 1 | 2 | 3 | m | … |
y | … | 4 | 3 | 2 | 2 | 2 | 3 | 4 | … |
①直接写出m的值;
②画出该函数图象,结合图象,得出当x= 时,y有最小值,y的最小值为 .
[解决问题]
(2)直接写出“问题情境”中问题的结论.