题目内容
我们知道,一元二次方程x2=-1没有实数根,即不存在一个实数的平方等于-1.若我们规定一个新数“i”,使其满足i2=-1(即方程x2=-1有一个根为i).并且进一步规定:一切实数可以与新数进行四则运算,且原有运算律和运算法则仍然成立,于是有i1=i,i2=-1,i3=i2•i=(-1)•i=-i,i4=(i2)2=(-1)2=1,从而对于任意正整数n,我们可以得到i4n+1=i4n•i=(i4)n•i=i,同理可得i4n+2=-1,i4n+3=-i,i4n=1.那么i+i2+i3+i4+…+i2012+i2013的值为 .
考点:解一元二次方程-直接开平方法,实数的运算
专题:新定义
分析:根据新定义得i4n+1=i,i4n+2=-1,i4n+3=-i,i4n=1,由于2012=4×503,所以i+i2+i3+i4+…+i2012+i2013=503(i-1-i+1)+i2012•i=i.
解答:解:∵i4n+1=i,i4n+2=-1,i4n+3=-i,i4n=1,
∴i+i2+i3+i4+…+i2012+i2013=503(i-1-i+1)+i2012•i
=1•i
=i.
故答案为:i.
∴i+i2+i3+i4+…+i2012+i2013=503(i-1-i+1)+i2012•i
=1•i
=i.
故答案为:i.
点评:本题考查了解一元二次方程-直接开平方法:形如x2=p或(nx+m)2=p(p≥0)的一元二次方程可采用直接开平方的方法解一元二次方程.如果方程化成x2=p的形式,那么可得x=±p;如果方程能化成(nx+m)2=p(p≥0)的形式,那么nx+m=±p.

练习册系列答案
相关题目
 如图,直线AB,CD相交于点O,∠AOC+∠BOD=70°,则∠AOD=( )
如图,直线AB,CD相交于点O,∠AOC+∠BOD=70°,则∠AOD=( )| A、145° | B、135° |
| C、125° | D、115° |
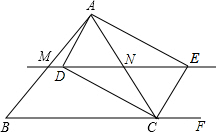 如图,线段MN是△ABC的中位线,CD、CE分别平分△ABC的内角∠ACB和外角∠ACF,CD、CE分别交直线MN于点D、E.
如图,线段MN是△ABC的中位线,CD、CE分别平分△ABC的内角∠ACB和外角∠ACF,CD、CE分别交直线MN于点D、E. 已知直角三角形ABO中,∠OAB=90°,OB=6,C为AB的中点,双曲线
已知直角三角形ABO中,∠OAB=90°,OB=6,C为AB的中点,双曲线 如图,直线AB、CD相交于点0,∠AOC=45°,则∠BOD=
如图,直线AB、CD相交于点0,∠AOC=45°,则∠BOD= 如图,直线a∥b,直线c与直线a、b相交,∠1=135°,∠2=
如图,直线a∥b,直线c与直线a、b相交,∠1=135°,∠2=