题目内容
将△ABD沿CE折叠，使点D与点A重合，得到如图所示的情形，如果此时AB=BC，∠B=40°，则∠D的度数为
- A.30°
- B.35°
- C.60°
- D.50°
B
分析：根据三角形的内角和定理以及等腰三角形的性质，得∠ACB=∠BAC=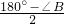
=70°；根据折叠的性质，得∠CAD=∠D，再根据三角形的外角的性质即可求解．
解答：∵AB=BC，∠B=40°，
∴∠ACB=∠BAC=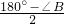=70°．
根据折叠的性质，得∠CAD=∠D．
又∠ACB=∠D+∠CAD，
∴∠CAD=∠D=35°．
故选B．
点评：此题综合运用了三角形的内角和定理及推论、等腰三角形的性质．
分析：根据三角形的内角和定理以及等腰三角形的性质，得∠ACB=∠BAC=
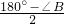=70°；根据折叠的性质，得∠CAD=∠D，再根据三角形的外角的性质即可求解．解答：∵AB=BC，∠B=40°，
∴∠ACB=∠BAC=
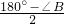=70°．根据折叠的性质，得∠CAD=∠D．
又∠ACB=∠D+∠CAD，
∴∠CAD=∠D=35°．
故选B．
点评：此题综合运用了三角形的内角和定理及推论、等腰三角形的性质．
练习册系列答案
出彩同步大试卷系列答案
相关题目
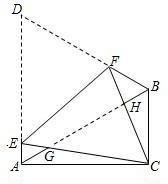线EF折叠，使D与C重合，CE与CF分别交AB于点G、H．
将△ABD沿CE折叠，使点D与点A重合，得到如图所示的情形，如果此时AB=BC，∠B=40°，则∠D的度数为（ ）| A、30° | B、35° | C、60° | D、50° |
如图，在△ABC中，∠BAC=126°，AD⊥BC于点D，将△ABD沿AD折叠，点B落在DC上的点E处，若AB=CE，则∠C=________．