题目内容
20. 如图,小明在大楼的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,已知该山坡的坡角∠ABC=30°点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上,且PH⊥HC.
如图,小明在大楼的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,已知该山坡的坡角∠ABC=30°点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上,且PH⊥HC.(1)山坡AB的坡度为1:$\sqrt{3}$;
(2)若山坡AB的长为20米,求大楼的窗口P处距离地面的高度.
分析 (1)坡角的正切函数值即为坡度,依此即可求解;
(2)先利用平行线的性质得出∠PBH=∠DPB=60°,由平角的定义求出∠ABP=180°-∠ABC-∠PBH=90°.再证明△ABP是等腰直角三角形,那么BP=AB=20米,然后在直角△PBH中利用三角函数即可求解.
解答 解:(1)∵山坡的坡角∠ABC=30°,
∴山坡AB的坡度为tan30°=$\frac{\sqrt{3}}{3}$=1:$\sqrt{3}$; (2)由题意得PD∥HC,AB⊥BP,PH⊥HC,∠DPA=15°,∠DPB=60°,AB=20米.
(2)由题意得PD∥HC,AB⊥BP,PH⊥HC,∠DPA=15°,∠DPB=60°,AB=20米.
∵PD∥HC,
∴∠PBH=∠DPB=60°,
∴∠ABP=180°-∠ABC-∠PBH=180°-30°-60°=90°.
在Rt△ABP中,∵∠ABP=90°,∠APB=60°-15°=45°,
∴BP=AB=20米,
在Rt△PBA中,∵∠PHB=90°,∠PBH=60°,
∴PH=PB•sin∠PBH=20×$\frac{\sqrt{3}}{2}$=10$\sqrt{3}$(米).
答:大楼的窗口P处距离地面的高度为10$\sqrt{3}$米.
故答案为1:$\sqrt{3}$.
点评 本题考查了解直角三角形的应用-仰角俯角问题,以及坡度坡角问题,其中涉及到平行线的性质,等腰直角三角形的判定与性质,正确利用三角函数是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.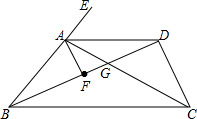 如图,BD平分∠ABC,AF平分∠BAD,∠EAD=2∠DBC,∠BDC=∠AFB,下列结论:①AD∥BC;②∠AFB=90°;③∠FAG=∠DCG,其中正确的是( )
如图,BD平分∠ABC,AF平分∠BAD,∠EAD=2∠DBC,∠BDC=∠AFB,下列结论:①AD∥BC;②∠AFB=90°;③∠FAG=∠DCG,其中正确的是( )
 如图,BD平分∠ABC,AF平分∠BAD,∠EAD=2∠DBC,∠BDC=∠AFB,下列结论:①AD∥BC;②∠AFB=90°;③∠FAG=∠DCG,其中正确的是( )
如图,BD平分∠ABC,AF平分∠BAD,∠EAD=2∠DBC,∠BDC=∠AFB,下列结论:①AD∥BC;②∠AFB=90°;③∠FAG=∠DCG,其中正确的是( )| A. | ①②③ | B. | ①② | C. | ① | D. | ②③ |
9.已知二次函数y=a(x+1)2+b有最大值0.1,则a与b的大小关系为( )
| A. | a>b | B. | a<b | C. | a=b | D. | 不能确定 |
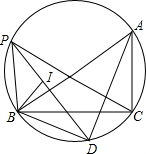 如图,在Rt△ABC中,∠BCA=90°,∠BAC的平分线交△ABC外接圆于点D,连接BD,若AB=2AC=4.
如图,在Rt△ABC中,∠BCA=90°,∠BAC的平分线交△ABC外接圆于点D,连接BD,若AB=2AC=4.