题目内容
20.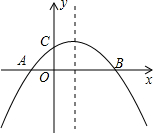 如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC.则下列结论:①abc<0;②ac-b+1=0;③OA•OB=-$\frac{c}{a}$.其中正确结论的个数是( )
如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC.则下列结论:①abc<0;②ac-b+1=0;③OA•OB=-$\frac{c}{a}$.其中正确结论的个数是( )| A. | 3 | B. | 0 | C. | 2 | D. | 1 |
分析 由抛物线开口方向得a<0,由抛物线的对称轴位置可得b>0,由抛物线与y轴的交点位置可得c>0,则可对①进行判断;利用OA=OC可得到A(-c,0),再把A(-c,0)代入y=ax2+bx+c得ac2-bc+c=0,两边除以c则可对②进行判断;设A(x1,0),B(x2,0),则OA=-x1,OB=x2,根据抛物线与x轴的交点问题得到x1和x2是方程ax2+bx+c=0(a≠0)的两根,利用根与系数的关系得到x1•x2=$\frac{c}{a}$,于是OA•OB=-$\frac{c}{a}$,则可对③进行判断.
解答 解:∵抛物线开口向下,
∴a<0,
∵抛物线的对称轴在y轴的右侧,
∴b>0,
∵抛物线与y轴的交点在x轴上方,
∴c>0,
∴abc<0,所以①正确;
∵C(0,c),OA=OC,
∴A(-c,0),
把A(-c,0)代入y=ax2+bx+c得ac2-bc+c=0,
∴ac-b+1=0,所以②正确;
设A(x1,0),B(x2,0),
∵二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,
∴x1和x2是方程ax2+bx+c=0(a≠0)的两根,
∴x1•x2=$\frac{c}{a}$,
∴OA•OB=-$\frac{c}{a}$,所以③正确.
故选:B.
点评 本题考查了二次函数图象与系数的关系:对于二次函数y=ax2+bx+c(a≠0),二次项系数a决定抛物线的开口方向和大小:当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右(简称:左同右异);常数项c决定抛物线与y轴交点:抛物线与y轴交于(0,c);抛物线与x轴交点个数由△决定:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

 全能测控期末小状元系列答案
全能测控期末小状元系列答案| A. | 60° | B. | 30° | C. | 60°和120° | D. | 30°和150° |
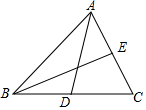 如图,AD和BE是△ABC的两条中线,设△ABD的面积为S1,△BCE的面积为S2,那么( )
如图,AD和BE是△ABC的两条中线,设△ABD的面积为S1,△BCE的面积为S2,那么( )| A. | S1>S2 | B. | S1=S2 | C. | S1<S2 | D. | 不能确定 |
| A. | 5 | B. | $\frac{8}{5}$ | C. | 6 | D. | -$\frac{8}{3}$ |
| A. | xy+3x=7 | B. | $\frac{1}{x}+y=5$ | C. | 2x-y=2 | D. | x2+y=1 |
| A. | 50° | B. | 55° | C. | 65° | D. | 75° |
| A. | 4 | B. | ±7 | C. | -7 | D. | 49 |
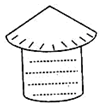 如图,粮仓的顶部是圆锥开关,这个圆锥底面圆半径长为3m,母线长为6m,为防止雨水,需在粮仓顶部铺上油毡,如果油毡的市场价是每平方米10元钱,那么购买油毡所需要的费用是108元.
如图,粮仓的顶部是圆锥开关,这个圆锥底面圆半径长为3m,母线长为6m,为防止雨水,需在粮仓顶部铺上油毡,如果油毡的市场价是每平方米10元钱,那么购买油毡所需要的费用是108元.