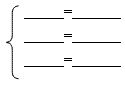题目内容
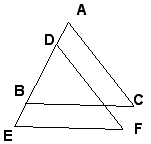
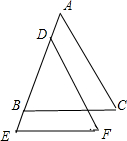 已知:如图BC∥EF,BC=EF,AB=DE;说明AC与EF相等.
已知:如图BC∥EF,BC=EF,AB=DE;说明AC与EF相等.
解:∵BC∥EF(已知)
∴∠ABC=∠________(________)
在△ABC和△DEF中
________
________
________
∴△ABC≌________(________)
∴AC=DF (________).
DEF 两直线平行,同位角相等) AB=DE, ∠ABC=∠DEF, BC=EF △DEF SAS 对应边相等
分析:根据两直线平行,同位角相等,可得出∠ABC=∠DEF,再利用SAS求证△ABC≌△DEF,然后利用其对边相等即可得出结论.
解答:∵BC∥EF(已知)
∴∠ABC=∠DEF ( 两直线平行,同位角相等)
在△ABC和△DEF中
∵AB=DE,
∠ABC=∠DEF,
BC=EF
∴△ABC≌△DEF ( SAS)
∴AC=DF (对应边相等).
故答案为:∠DEF; ( 两直线平行,同位角相等);
AB=DE,
∠ABC=∠DEF,
BC=EF;
△DEF ( SAS);
(对应边相等).
点评:此题主要考查学生对全等三角形的判定与性质这一知识点的理解和掌握,这是以后做题的基础,一定要熟练掌握才行.
分析:根据两直线平行,同位角相等,可得出∠ABC=∠DEF,再利用SAS求证△ABC≌△DEF,然后利用其对边相等即可得出结论.
解答:∵BC∥EF(已知)
∴∠ABC=∠DEF ( 两直线平行,同位角相等)
在△ABC和△DEF中
∵AB=DE,
∠ABC=∠DEF,
BC=EF
∴△ABC≌△DEF ( SAS)
∴AC=DF (对应边相等).
故答案为:∠DEF; ( 两直线平行,同位角相等);
AB=DE,
∠ABC=∠DEF,
BC=EF;
△DEF ( SAS);
(对应边相等).
点评:此题主要考查学生对全等三角形的判定与性质这一知识点的理解和掌握,这是以后做题的基础,一定要熟练掌握才行.

练习册系列答案
相关题目
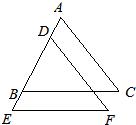 23、已知:如图BC∥EF,BC=EF,AD=BE,试说明AC与DF的关系.
23、已知:如图BC∥EF,BC=EF,AD=BE,试说明AC与DF的关系.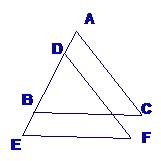 23、已知:如图BC∥EF,BC=EF,AB=DE;说明AC与EF相等.
23、已知:如图BC∥EF,BC=EF,AB=DE;说明AC与EF相等. 已知:如图BC∥EF,BC=EF,AD=BE,试说明AC与DF的关系.
已知:如图BC∥EF,BC=EF,AD=BE,试说明AC与DF的关系.