Question

【题目】把代数式通过配凑等手段，得到局部完全平方式，再进行有关运算和解题，这种解题方法叫做配方法．

如：①用配方法分解因式：a2+6a+8，

解：原式＝a2+6a+8+1﹣1＝a2+6a+9﹣1＝（a+2）（a+4）

②M＝a2﹣2ab+2b2﹣2b+2，利用配方法求M的最小值，

解：a2﹣2ab+2b2﹣2b+2＝a2﹣2ab+b2+b2﹣2b+1+1＝（a﹣b）2+（b﹣1）2+1

∵（a﹣b）2≥0，（b﹣1）2≥0

∴当a＝b＝1时，M有最小值1．

请根据上述材料解决下列问题：

（1）在横线上添加一个常数，使之成为完全平方式：x2﹣x+　 　．

（2）用配方法因式分解：x2﹣4xy+3y2．

（3）若M＝x2+2x﹣1，求M的最小值．

（4）已知x2+2y2+z2﹣2xy﹣2y﹣4z+5＝0，则x+y+z的值为　 　．

Answer 1

【答案】（1）；（2）（x﹣y）（x﹣3y）；（3）当x＝﹣4时，M有最小值为﹣5；（4）4．

【解析】

（1）加一次项系数一半的平方，可配成完全平方式；

（2）将3y2化成4y2y2，前三项配成完全平方式，再利用平方差公式进行因式分解；

（3）提取系数后，再加一次项系数一半的平方16，并减去16，配成完全平方式，可知M的最小值；

（4）拆项后配成三个完全平方式，利用非负数的性质求出x、y、z的值，然后相加即可．

解：（1）x2﹣x+＝，

故答案为：；

（2）x2﹣4xy+3y2

＝x2﹣4xy+4y2﹣y2

＝（x﹣2y）2﹣y2

＝（x﹣2y+y）（x﹣2y﹣y）

＝（x﹣y）（x﹣3y）；

（3）M＝x2+2x﹣1＝（x2+8x+16﹣16）﹣1＝（x+4）2﹣5，

∵（x+4）2≥0，

∴当x＝﹣4时，M有最小值为﹣5；

（4）∵x2+2y2+z2﹣2xy﹣2y﹣4z+5＝0，

∴x2﹣2xy+y2+y2﹣2y+1+z2﹣4z+4＝0，

∴（x﹣y）2+（y﹣1）2+（z﹣2）2＝0，

∴，

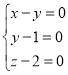∴x＝1，y＝1，z＝2，

∴x+y+z＝1+1+2＝4，

故答案为：4．