题目内容
(12分)如图1,在△ABC中,AC=AB=2,∠A=90°,将一块与△ABC全等的三角板的直角顶点放在点C上,一直角边与BC重叠.
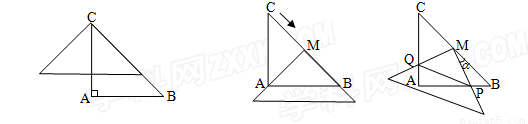
(1)操作1:固定△ABC,将三角板沿 方向平移,使其直角顶点落在BC的中点M,如图2所示,探究:三角板沿
方向平移,使其直角顶点落在BC的中点M,如图2所示,探究:三角板沿 方向平移的距离为___________;
方向平移的距离为___________;
(2)操作2:在(1)的情况下,将三角板BC的中点M顺时针方向旋转角度 ,如图3所示,探究:设三角形板两直角边分别与AB、AC交于点P、Q,观察四边形MPAQ形状的变化,问:四边形MPAQ的面积S是否改变,若不变,求其面积;若改变,试说明理由;
,如图3所示,探究:设三角形板两直角边分别与AB、AC交于点P、Q,观察四边形MPAQ形状的变化,问:四边形MPAQ的面积S是否改变,若不变,求其面积;若改变,试说明理由;
(3)在(2)的情形下,连PQ,设BP=x,记△MPQ的面积为y,试求y关于x的函数关系式,并求x为何值时,y的值是四边形MPAQ的面积的一半,此时,指出四边形MPAQ的形状.
(1) ;(2)不变,1;(2)
;(2)不变,1;(2) ,当
,当 时,MPAQ为正方形.
时,MPAQ为正方形.
【解析】
试题分析:(1)M是BC的中点,三角板沿C→B方向平移的距离为CM,根据勾股定理可求BC,那么CM可求;
(2)连AM,分别证明△MAQ≌△MBP和△MAP≌△MCQ,那么四边形MPAQ的面积S就是△ABC面积的一半;
(3)用四边形MPAQ的面积减去△APQ可得△MPQ的面积,而AQ=PB=x,AP=2﹣x,据此列出y关于x的函数关系式,将函数值代入函数关系式可得自变量,根据自变量可以判断四边形MPAQ的形状.
试题解析:(1)BC= ,∴CM=
,∴CM= BC=
BC= ,故三角板沿C→B方向平移的距离为:
,故三角板沿C→B方向平移的距离为: ;
;
(2)四边形MPAQ的面积S不变,如图,连AM,M是等腰直角三角形ABC斜边BC的中点,

∴AM=BM,而∠QMA=∠PMB=a,∠QAM=∠PBM=45°,∴△MAQ≌△MBP,
同理可得:△MAP≌△MCQ,
∴S四边形MPAQ=S△MAQ+S△MAP= S△ABC=
S△ABC= ;
;
(3) ,如果y的值是四边形MPAQ的面积的一半,
,如果y的值是四边形MPAQ的面积的一半,
则有: ,解得,
,解得, .
.
当 时,即BP=1,∵AB=2,∴AP=1,
时,即BP=1,∵AB=2,∴AP=1,
∵y的值是四边形MPAQ的面积的一半,∴△PAQ的面积=△PMQ的面积= ,∴QA=1,
,∴QA=1,
∵△MAQ≌△MBP,∴QM=MP,∴QM=MP=1,∴QM=MP=QA=AP=1,
∵∠PAQ=90°,∴四边形MPAQ为正方形.
考点:1.旋转的性质;2.全等三角形的判定与性质;3.正方形的判定;4.平移的性质.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 (
(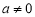 )的图象过正方形ABOC的三顶点A、B、C,则
)的图象过正方形ABOC的三顶点A、B、C,则 的值是 .
的值是 .



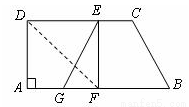
 是方程
是方程 的解,则k的值是 ;
的解,则k的值是 ; 元,买一个篮球需要
元,买一个篮球需要 元,则买4个足球、7个篮球共需要( )元。
元,则买4个足球、7个篮球共需要( )元。