题目内容
 (2008•武汉模拟)如图,正方形ABCD的边BC在x轴负半轴上,E(-
(2008•武汉模拟)如图,正方形ABCD的边BC在x轴负半轴上,E(-| 6 |
| k |
| x |
-3
-3
.分析:根据正方形的性质,设出D(a,2n),代入反比例函数解析式;再将E(-
,n)代入反比例函数解析式,二者结合即可求出k的值.
| 6 |
解答:解:∵E(-
,n),四边形ABCD是正方形,
∴设D(a,2n),
∴2an=k,
∵-
n=k,
则a=-
,
∴可知正方形边长是
,
∴n=
,
∴k=-3.
| 6 |
∴设D(a,2n),
∴2an=k,
∵-
| 6 |
则a=-
| ||
| 2 |
∴可知正方形边长是
| 6 |
∴n=
| ||
| 2 |
∴k=-3.
点评:本题考查了反比例函数图象上点的坐标特征和正方形的性质,要知道,所有在反比例函数上的点的横纵坐标的积应等于比例系数.

练习册系列答案
相关题目
 (2008•武汉模拟)如图,在高为2m,坡角为30°的楼梯上铺地毯,地毯的长度至少应为( )
(2008•武汉模拟)如图,在高为2m,坡角为30°的楼梯上铺地毯,地毯的长度至少应为( )
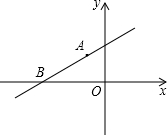 (2008•武汉模拟)如图,直线y=kx+b经过A(-1,1)和B(-
(2008•武汉模拟)如图,直线y=kx+b经过A(-1,1)和B(-