题目内容
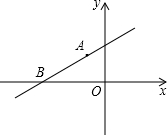（2008•武汉模拟）如图，直线y=kx+b经过A（-1，1）和B（-| 7 |
-
＜x＜-1
| 7 |
-
＜x＜-1
．| 7 |
分析：先把A（-1，1）和B（-
，0）两点代入一次函数关系式，求出k、b的值，再解不等式组-x＞kx+b＞0即可．
| 7 |
解答：解：解法一：∵直线y=kx+b经过A（-1，1）和B（-0）两点，
∴
，解得
，
∴直线解析式为：y=
x+
，
∵-x＞kx+b＞0，
∴0＜
x+
＜-x，解得：-
＜x＜-1．
解法二：∵A（-1，1）和B（-
，0），
∴由函数图象可知，当x＞-
时，直线在x轴的上方，即kx+b＞0，
当-
＜x＜-1时，不等式-x＞kx+b＞0成立．
故答案为：-
＜x＜-1．
∴
|
|
∴直线解析式为：y=
| ||
| 6 |
| ||
| 6 |
∵-x＞kx+b＞0，
∴0＜
| ||
| 6 |
| ||
| 6 |
| 7 |
解法二：∵A（-1，1）和B（-
| 7 |
∴由函数图象可知，当x＞-
| 7 |
当-
| 7 |
故答案为：-
| 7 |
点评：本题考查了用待定系数法求一次函数的解析式及一元一次不等式组的解法．正确的求出k与b的值是解题的关键．
练习册系列答案
相关题目
（2008•武汉模拟）如图，在高为2m，坡角为30°的楼梯上铺地毯，地毯的长度至少应为（ ）