题目内容
 在边长为1的正方形ABCD中,当第1次作AO⊥BD,第2次作EO⊥AD;第3次作EF⊥AO,…依此方法继续作垂直线段,当作到第n次时,所得的最小的三角形的面积是________(用含n的代数式表示).
在边长为1的正方形ABCD中,当第1次作AO⊥BD,第2次作EO⊥AD;第3次作EF⊥AO,…依此方法继续作垂直线段,当作到第n次时,所得的最小的三角形的面积是________(用含n的代数式表示).

分析:根据正方形的性质可得AB=AD,然后根据等腰直角三角形的性质求出△AOD的面积,再求出△AOE的面积,△AEF的面积,根据计算结果可得下一次得到最小的三角形的面积是上一次三角形的
 ,然后写出第n次时所得的最小的三角形的面积即可.
,然后写出第n次时所得的最小的三角形的面积即可.解答:∵四边形ABCD是正方形,边长为1,
∴AB=AD,正方形的面积为1,
第1次作AO⊥BD,则最小△AOD的面积=
 ×
× =
= =
= ,
,第2次作EO⊥AD,最小△AOE的面积=
 ×
× =
= =
= ;
;第3次作EF⊥AO,最小△AEF的面积=
 ×
× =
= ,
,…,
依此类推,作到第n次时,最小三角形的面积=
 .
.故答案为:
 .
.点评:本题考查了正方形的性质,等腰直角三角形的性质,等腰三角形三线合一的性质,观察出下一次得到最小的三角形的面积是上一次三角形的
 是解题的关键.
是解题的关键. 
练习册系列答案
相关题目
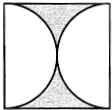 如图,在边长为a的正方形铁块中,以两对边中点为圆心,以a为直径截取两个半圆,求余下废料的面积是多少?
如图,在边长为a的正方形铁块中,以两对边中点为圆心,以a为直径截取两个半圆,求余下废料的面积是多少?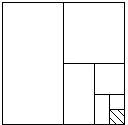 我国著名的数学家华罗庚曾说过:“数形结合百般好,割裂分家万事非”,如图,在边长为1的正方形纸板上,依次贴上面积为
我国著名的数学家华罗庚曾说过:“数形结合百般好,割裂分家万事非”,如图,在边长为1的正方形纸板上,依次贴上面积为
 在边长为16cm的正方形纸片的四个角各剪去一个同样大小的正方形,折成一个无盖的长方体.
在边长为16cm的正方形纸片的四个角各剪去一个同样大小的正方形,折成一个无盖的长方体.