题目内容
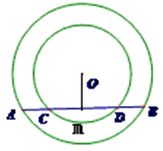
如图,在平面直角坐标系xOy中,直线AB经过点A(-4,0)、B(0,4),⊙O的半径为1(O为坐标原点),点P在直线AB上,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为( )

A. | B. | C.2 | D.3 |
B.
试题分析:如图,过点O作OP1⊥AB,过点P1作⊙O的切线交⊙O于点Q1,连接OQ,OQ1.
当PQ⊥AB时,易得四边形P1PQO是矩形,即PQ=P1O.
∵P1Q1是⊙O的切线, ∴∠OQ1P1=900.
∴在Rt△OP1Q1中,P1Q1<P1O,∴P1Q1即是切线长PQ的最小值.
∵A(-4,0),B(0,4),∴OA=OB=4.
∴△OAB是等腰直角三角形. ∴△AOP1是等腰直角三角形.
根据勾股定理,得OP1=
 .
.∵⊙O的半径为1,∴OQ1=1.
根据勾股定理,得P1Q1=
 .
.故选B.


练习册系列答案
相关题目
 .
.
 ;
; ,∴AB=
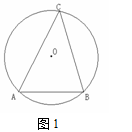
,∴AB= ),C为直线AB上一点,过A、O、C的⊙E的半径为2.求线段OC的长.
),C为直线AB上一点,过A、O、C的⊙E的半径为2.求线段OC的长.
 ,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB,AC于E,F,连结EF, 设⊙O半径为x, EF为y.①y关于x的函数关系式;②求线段EF长度的最小值.
,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB,AC于E,F,连结EF, 设⊙O半径为x, EF为y.①y关于x的函数关系式;②求线段EF长度的最小值.