Question

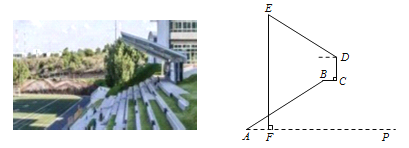
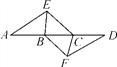
【题目】如图，点A，B，C，D在同一条直线上，点E，F分别在直线AD的两侧，且AE＝DF，∠A＝∠D，AB＝DC.

(1)求证：△AEC≌△DFB；

(2)若∠EBD＝60°，BE＝BC，求证：四边形BFCE是菱形．

Answer 1

【答案】（1）证明见解析（2）证明见解析

【解析】(1)、根据题意得出AC=BD，结合∠A=∠D，AE=DF，从而得出三角形全等；(2)、根据全等得出EC＝BF，∠ECA＝∠FBD，从而得出EC∥BF，则四边形为平行四边形，结合等边三角形的性质得出BE=BC，△EBC为等边三角形，从而得出菱形．

(1)∵AB＝DC，∴AB＋BC＝DC＋BC.即AC＝DB.

在△ACE和△DBF中，∴△ACE≌△DBF(SAS)；

(2)∵△ACE≌△DBF，∴EC＝BF，∠ECA＝∠FBD.

∴EC∥BF，∴四边形BFCE是平行四边形．∵∠EBD＝60°，BE＝BC，

∴△EBC是等边三角形，∴EB＝EC，∴四边形BFCE是菱形．