Question

已知平面直角坐标系上有一点A（1，1），将点A绕原点按顺时针方向旋转45°，得到点A₁的坐标为

1. A.
   （，0）
2. B.
   （1，0）
3. C.
   （0，1）
4. D.
   （0，）

Answer 1

A
分析：根据勾股定理列式求出OA的长，再根据点A的坐标判断出OA与x轴的夹角为45°，从而得到旋转后点A₁落在x轴正半轴上，即可得解．
解答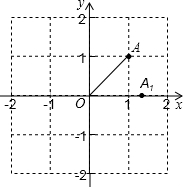：解：∵点A（1，1），
∴根据勾股定理可得OA==，
且OA与x轴的夹角为45°，
∴点A绕原点按顺时针方向旋转45°得到的点A₁在x轴正半轴，
∴点A₁的坐标为（，0）．
故选A．
点评：本题考查了坐标与图形的变化-旋转，根据旋转的性质判断出点A₁的位置是解题的关键，作出图形更形象直观．