题目内容
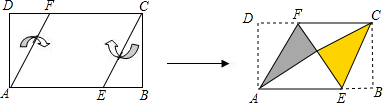
将矩形纸片ABCD按如图所示的方式折叠，得到菱形AECF．若AB=3，则BC的长为
- A.1
- B.2
- C.
- D.
D
分析：根据题意可知，AC=2BC，∠B=90°，所以根据勾股定理可知AC2=AB2+BC2，即（2BC）2=32+BC2，从而可求得BC的长．
解答：∵AC=2BC，∠B=90°，
∴AC2=AB2+BC2，
∴（2BC）2=32+BC2，
∴BC=．
故选D．
点评：此题主要考查学生对菱形的性质及勾股定理的理解及运用．
分析：根据题意可知，AC=2BC，∠B=90°，所以根据勾股定理可知AC2=AB2+BC2，即（2BC）2=32+BC2，从而可求得BC的长．
解答：∵AC=2BC，∠B=90°，
∴AC2=AB2+BC2，
∴（2BC）2=32+BC2，
∴BC=
．故选D．
点评：此题主要考查学生对菱形的性质及勾股定理的理解及运用．
练习册系列答案
波波熊暑假作业江西人民出版社系列答案
学而优暑期衔接南京大学出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
将矩形纸片ABCD按如图所示的方式折叠，得到菱形AECF．若AB=3，则BC的长为（ ）
| A、1 | ||
| B、2 | ||
C、
| ||
D、
|
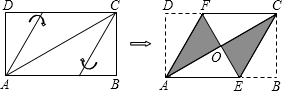C的长为
