题目内容
能力题:
(1)已知a为实数,化简:
-a
,阅读下面的解答过程,请判断是否正确?若不正确,请写出正确的解答过程:
解:
-a
=a
-a•
=(a-1)
(2)若x、y为实数,且y=
,求
•
的值.
(1)已知a为实数,化简:
| -a3 |
-
|
解:
| -a3 |
-
|
| -a |
| 1 |
| a |
| -a |
| -a |
(2)若x、y为实数,且y=
| ||||
| x+2 |
| x+y |
| x-y |
考点:二次根式的混合运算
专题:计算题
分析:(1)根据二次根有意义的条件得到a<0,则利用二次根式的性质化简得原式=(-a)
-a•
•
,然后约分后合并即可;
(2)根据二次根有意义的条件得到x2-4=0,解得x=2或x=-2,由于分母不为0,则x=2,y=
,然后把x和y的值代入原式进行计算.
| -a |
| 1 |
| -a |
| -a |
(2)根据二次根有意义的条件得到x2-4=0,解得x=2或x=-2,由于分母不为0,则x=2,y=
| 1 |
| 4 |
解答:解:(1)不正确.
正确的解答过程为:原式=(-a)
-a•
•
=(-a+1)
;
(2)∵x2-4≥0且4-x2≥0,
∴x2-4=0,解得x=2或x=-2,
∵x+2≠0,
∴x=2,
∴y=
,
∴原式=
=
=
.
正确的解答过程为:原式=(-a)
| -a |
| 1 |
| -a |
| -a |
| -a |
(2)∵x2-4≥0且4-x2≥0,
∴x2-4=0,解得x=2或x=-2,
∵x+2≠0,
∴x=2,
∴y=
| 1 |
| 4 |
∴原式=
| x2-y2 |
22-(
|
| ||
| 4 |
点评:本题考查了二次根式的混合运算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.

练习册系列答案
相关题目
下列条件中,不能判定以A′、B′、C′为顶点的三角形与△ABC相似的是( )
| A、∠C=∠C′=90°,∠B=∠A′=50° | ||||
| B、AB=AC,A′B′=A′C′,∠B=∠B′ | ||||
C、∠B=∠B′,
| ||||
D、∠A=∠A′,
|
下列各式计算正确的是( )
A、
| ||
B、±
| ||
C、
| ||
D、
|

 如图,作字母N(折线ABCD)关于y轴的轴对称图形,并写出所得图形相对应的坐标.
如图,作字母N(折线ABCD)关于y轴的轴对称图形,并写出所得图形相对应的坐标.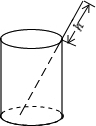 如图,将一根长12厘米的筷子置于底面直径为6厘米,高为8厘米的圆柱形杯子中,则筷子露在杯子外面的长度至少为
如图,将一根长12厘米的筷子置于底面直径为6厘米,高为8厘米的圆柱形杯子中,则筷子露在杯子外面的长度至少为