题目内容
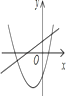
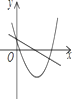
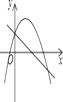
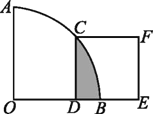
【题目】如图，矩形OABC的顶点A、C分别在x轴、y轴上，OA＝4，OC＝3，直线m：y＝﹣
x从原点O出发，沿x轴正方向以每秒1个单位长度的速度运动，设直线m与矩形OABC的两边分别交于点M，N，直线m运动的时间为t(秒)，设△OMN的面积为S，则能反映S与t之间函数关系的大致图象是( )
A. 
B. 
C. 
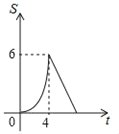D.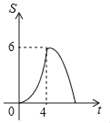 
【答案】D
【解析】
分两种情形①如图1中，当0＜t≤4时，②如图2中，当4＜t≤8时，分别求出y与t的函数关系式即可解决问题．
如图1中，当0＜t≤4时，
∵MN∥CA，
∴OM：OA＝ON：OC，
∴OM：ON＝OA：OC＝4：3，
∴OM＝t，ON＝
t，
∴y＝
t2．
如图2中，当4＜t≤8时，
y＝S△EOF﹣S△EON﹣S△OFM＝
综上所述y＝
．
故选：D．
练习册系列答案
特高级教师点拨系列答案
相关题目
