题目内容
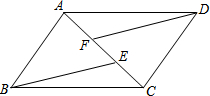 如图,已知点A、F、E、C在同一直线上,AB∥CD,AF=CE,∠ABE=∠CDF.
如图,已知点A、F、E、C在同一直线上,AB∥CD,AF=CE,∠ABE=∠CDF.(1)写出图中所有全等三角形;
(2)从(1)中任选一组进行证明.
考点:全等三角形的判定
专题:
分析:(1)根据题目所给条件可得△ABE≌△CDF,△ADF≌△CBE,△ADC≌△CBA;
(2)首先根据等式的性质可得AE=CF,再根据平行线的性质可得∠BAE=∠DCF,再加上∠ABE=∠CDF可利用AAS证明△ABE≌△CDF.
(2)首先根据等式的性质可得AE=CF,再根据平行线的性质可得∠BAE=∠DCF,再加上∠ABE=∠CDF可利用AAS证明△ABE≌△CDF.
解答:解:(1)△ABE≌△CDF,△ADF≌△CBE,△ADC≌△CBA;
(2)△ABE≌△CDF;
理由:∵AF=CE,
∴AE=CF,
∵AB∥CD,
∴∠BAE=∠DCF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(AAS).
(2)△ABE≌△CDF;
理由:∵AF=CE,
∴AE=CF,
∵AB∥CD,
∴∠BAE=∠DCF,
在△ABE和△CDF中,
|
∴△ABE≌△CDF(AAS).
点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
相关题目
已知点M到x轴的距离为3,到y轴距离为2,且在第四象限内,则点M的坐标为( )
| A、(2,3) |
| B、(2,-3) |
| C、(3,2) |
| D、不能确定 |
下列命题中正确的是( )
| A、一边和两角分别相等的两个三角形全等 |
| B、顶角与底边对应相等的两个等腰三角形全等 |
| C、斜边上的中线对应相等的两个直角三角形全等 |
| D、两边和其中一边的对角对应相等的两个三角形全等 |
 如图,将两张长为8,宽为2的矩形纸条交叉,使重叠部分是一个菱形,容易知道当两张纸条垂直时,菱形的周长有最小值8,那么菱形周长的最大值是( )
如图,将两张长为8,宽为2的矩形纸条交叉,使重叠部分是一个菱形,容易知道当两张纸条垂直时,菱形的周长有最小值8,那么菱形周长的最大值是( )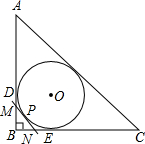 如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D、E,过劣弧DE(不包括端点D,E)上任一点P作⊙O的切线MN与AB,BC分别交于点M,N,若⊙O的半径为4cm,则Rt△MBN的周长为
如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D、E,过劣弧DE(不包括端点D,E)上任一点P作⊙O的切线MN与AB,BC分别交于点M,N,若⊙O的半径为4cm,则Rt△MBN的周长为