题目内容
 如图,点A是x轴正半轴上的动点,点B的坐标为(0,4),将线段AB的中点绕点A按顺时针方向旋转90°得点C,过点C作x轴的垂线,垂足为F,过点B作y轴的垂线与直线CF相交于点E,点D是点A关于直线CF的对称点,连接AC、BC、CD,设点A的横坐标为t.
如图,点A是x轴正半轴上的动点,点B的坐标为(0,4),将线段AB的中点绕点A按顺时针方向旋转90°得点C,过点C作x轴的垂线,垂足为F,过点B作y轴的垂线与直线CF相交于点E,点D是点A关于直线CF的对称点,连接AC、BC、CD,设点A的横坐标为t.(I)线段AB与AC的数量关系是
(II)当t=2时,求CF的长;
(III)当t为何值时,点C落在线段BD上?求出此时点C的坐标;
(IV)设△BCE的面积为S,求S与t之间的函数关系式.
考点:相似形综合题
专题:
分析:(I)根据“线段AB的中点绕点A按顺时针方向旋转90°得点C”推知AB与AC的关系;
(II)由Rt△ACF∽Rt△BAO,得CF=
OA=
t,由此求出CF的值;
(III)由Rt△ACF∽Rt△BAO,可以求得AF的长度;若点C落在线段BD上,则有△DCF∽△DBO,根据相似比例式列方程求出t的值;
(IV)有三种情况,需要分类讨论:当0<t≤8时,如题图1所示;当t>8时,如答图1所示;t=8时.
(II)由Rt△ACF∽Rt△BAO,得CF=
| 1 |
| 2 |
| 1 |
| 2 |
(III)由Rt△ACF∽Rt△BAO,可以求得AF的长度;若点C落在线段BD上,则有△DCF∽△DBO,根据相似比例式列方程求出t的值;
(IV)有三种情况,需要分类讨论:当0<t≤8时,如题图1所示;当t>8时,如答图1所示;t=8时.
解答: 解:(I)∵如图,将线段AB的中点绕点A按顺时针方向旋转90°得点C,
解:(I)∵如图,将线段AB的中点绕点A按顺时针方向旋转90°得点C,
∵AB=2AC,∠BAC=90°,
∴AB⊥AC.
故答案是:AB=2AC,AB⊥AC;
(II)由题意,易证Rt△ACF∽Rt△BAO,
∴
=
.
∵AB=2AM=2AC,
∴CF=
OA=
t.
当t=2时,CF=1;
(III)由(1)知,Rt△ACF∽Rt△BAO,
∴
=
,
∴AF=
OB=2,∴FD=AF=2,.
∵点C落在线段BD上,
∴△DCF∽△DBO,
∴
=
,即
=
,
整理 得t2+4t-16=0
解得 t=2
-2或t=-2
-2(不合题意,舍去)
∴当t=2
-2时,点C落在线段BD上.
此时,CF=
t=
-1,
OF=t+2=2
,
∴点C的坐标为(2
,-1+
);
(IV)①当0<t≤8时,如题图1所示:
S=
BE•CE=
(t+2)•(4-
t)=-
t2+
t+4;
②当t>8时,如答图1所示:CE=CF-EF=
t-4
S=
BE•CE=
(t+2)•(
t-4)=
t2-
t-4;
③如答图2,当点C与点E重合时,CF=OB=4,可得t=OA=8,此时S=0.
 解:(I)∵如图,将线段AB的中点绕点A按顺时针方向旋转90°得点C,
解:(I)∵如图,将线段AB的中点绕点A按顺时针方向旋转90°得点C,∵AB=2AC,∠BAC=90°,
∴AB⊥AC.
故答案是:AB=2AC,AB⊥AC;
(II)由题意,易证Rt△ACF∽Rt△BAO,
∴
| CF |
| OA |
| AC |
| AB |
∵AB=2AM=2AC,
∴CF=
| 1 |
| 2 |
| 1 |
| 2 |
当t=2时,CF=1;
(III)由(1)知,Rt△ACF∽Rt△BAO,

∴
| AF |
| OB |
| AC |
| AB |
∴AF=
| 1 |
| 2 |
∵点C落在线段BD上,
∴△DCF∽△DBO,
∴
| CF |
| OB |
| DF |
| OD |
| ||
| 4 |
| 2 |
| t+4 |
整理 得t2+4t-16=0
解得 t=2
| 5 |
| 5 |
∴当t=2
| 5 |
此时,CF=
| 1 |
| 2 |
| 5 |
OF=t+2=2
| 5 |
∴点C的坐标为(2
| 5 |
| 5 |

(IV)①当0<t≤8时,如题图1所示:
S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 2 |
②当t>8时,如答图1所示:CE=CF-EF=
| 1 |
| 2 |
S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 2 |
③如答图2,当点C与点E重合时,CF=OB=4,可得t=OA=8,此时S=0.
点评:本题考查了坐标平面内几何图形的多种性质,是一道难度较大的中考压轴题.涉及到的知识点包括相似三角形、全等三角形、点的坐标、几何变换(旋转、平移、对称)等,非常全面;分类讨论的思想贯穿第(2)问.本题涉及考点众多,内涵丰富,对考生的数学综合能力要求较高.

练习册系列答案
相关题目
 如图,E为正方形ABCD内一点,∠AEB=135°,BE=3cm,△AEB按顺时针方向旋转一个角度后成为△CFB,则旋转_____度,EF=_____cm( )
如图,E为正方形ABCD内一点,∠AEB=135°,BE=3cm,△AEB按顺时针方向旋转一个角度后成为△CFB,则旋转_____度,EF=_____cm( )A、80,
| ||
B、70,
| ||
C、90,3
| ||
D、70,3
|
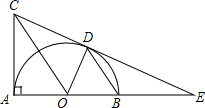 如图,已知BD是以O为圆心,AB长为直径的半圆的弦,AC⊥AB,BD∥OC,直线CD交AB的延长线于点E.
如图,已知BD是以O为圆心,AB长为直径的半圆的弦,AC⊥AB,BD∥OC,直线CD交AB的延长线于点E. 如图,已知直径为1个单位长度的圆形纸片上的点A与数轴上表示-1的点重合,若将该圆形纸片沿数轴顺时针滚动一周(无滑动)后点A与数轴上的点A′重合,则点A′表示的数为
如图,已知直径为1个单位长度的圆形纸片上的点A与数轴上表示-1的点重合,若将该圆形纸片沿数轴顺时针滚动一周(无滑动)后点A与数轴上的点A′重合,则点A′表示的数为 用等腰直角三角板画∠AOB=45°,并将三角板沿OB方向平移到如图的虚线处后绕点M逆时针方向旋转25°,则三角板的斜边与射线OA的夹角α为
用等腰直角三角板画∠AOB=45°,并将三角板沿OB方向平移到如图的虚线处后绕点M逆时针方向旋转25°,则三角板的斜边与射线OA的夹角α为 如图,将一张边长为6的正方形纸片按虚线裁掉四个梯形后,剩下部分恰好围成一个底面是正三角形的棱柱,这个棱柱的侧面积为
如图,将一张边长为6的正方形纸片按虚线裁掉四个梯形后,剩下部分恰好围成一个底面是正三角形的棱柱,这个棱柱的侧面积为