题目内容
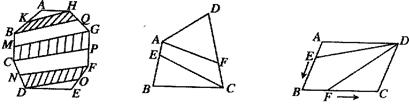
 如图,八边形ABCDEFGH中,∠A=∠B=∠C=∠D=∠E=∠F=∠G=∠H=135°,AB=CD=EF=GH=1cm,BC=DE=FG=HA=
如图,八边形ABCDEFGH中,∠A=∠B=∠C=∠D=∠E=∠F=∠G=∠H=135°,AB=CD=EF=GH=1cm,BC=DE=FG=HA= cm,则这个八边形的面积等于
cm,则这个八边形的面积等于
- A.7cm2
- B.8cm2
- C.9cm2
- D.14cm2
A
分析:延长四条不相邻的边,就可得到正方形,正方形的面积以四个直角三角形的面积的差,即为所求.
解答: 解:延长AB、DC交于M点,延长CD、FE交于N点,延长EF、HG交于P点,延长GH、BA交于Q点,则MNPQ是矩形,△BCM、△DEN、△FGP、△AHQ均为等腰直角三角形.这个八边形的面积等于=矩形面积-4个小三角形的面积=3×3-4×1×1÷2=7.
解:延长AB、DC交于M点,延长CD、FE交于N点,延长EF、HG交于P点,延长GH、BA交于Q点,则MNPQ是矩形,△BCM、△DEN、△FGP、△AHQ均为等腰直角三角形.这个八边形的面积等于=矩形面积-4个小三角形的面积=3×3-4×1×1÷2=7.
故选A.
点评:解决本题的关键根据所给条件把八边形补成正方形.
分析:延长四条不相邻的边,就可得到正方形,正方形的面积以四个直角三角形的面积的差,即为所求.
解答:
 解:延长AB、DC交于M点,延长CD、FE交于N点,延长EF、HG交于P点,延长GH、BA交于Q点,则MNPQ是矩形,△BCM、△DEN、△FGP、△AHQ均为等腰直角三角形.这个八边形的面积等于=矩形面积-4个小三角形的面积=3×3-4×1×1÷2=7.
解:延长AB、DC交于M点,延长CD、FE交于N点,延长EF、HG交于P点,延长GH、BA交于Q点,则MNPQ是矩形,△BCM、△DEN、△FGP、△AHQ均为等腰直角三角形.这个八边形的面积等于=矩形面积-4个小三角形的面积=3×3-4×1×1÷2=7.故选A.
点评:解决本题的关键根据所给条件把八边形补成正方形.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案
相关题目


 AB,CF=
AB,CF=

 AB,
AB, ABCD的面积是2,AB=a,BC=b,点E从点A出发沿AB以每秒v个单位长的速度向点B运动,点F从点B出发沿BC以每秒
ABCD的面积是2,AB=a,BC=b,点E从点A出发沿AB以每秒v个单位长的速度向点B运动,点F从点B出发沿BC以每秒 个单位长的速度向点C运动.E、F分别从点A、B同时出发,当其中一点到达端点时,另一点也随之停止运动.请问四边形DEBF的面积的值是否随着时间t的变化而变化?若不变,请写出这个值 ,并写出理由;若变化,说明是怎样变化的.
个单位长的速度向点C运动.E、F分别从点A、B同时出发,当其中一点到达端点时,另一点也随之停止运动.请问四边形DEBF的面积的值是否随着时间t的变化而变化?若不变,请写出这个值 ,并写出理由;若变化,说明是怎样变化的.

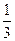 AB,
AB, ABCD的面积是2,AB=a,BC=b,点E从点A出发沿AB以每秒v个单位长的速度向点B运动,点F从点B出发沿BC以每秒
ABCD的面积是2,AB=a,BC=b,点E从点A出发沿AB以每秒v个单位长的速度向点B运动,点F从点B出发沿BC以每秒 个单位长的速度向点C运动.E、F分别从点A、B同时出发,当其中一点到达端点时,另一点也随之停止运动.请问四边形DEBF的面积的值是否随着时间t的变化而变化?若不变,请写出这个值 ,并写出理由;若变化,说明是怎样变化的.
个单位长的速度向点C运动.E、F分别从点A、B同时出发,当其中一点到达端点时,另一点也随之停止运动.请问四边形DEBF的面积的值是否随着时间t的变化而变化?若不变,请写出这个值 ,并写出理由;若变化,说明是怎样变化的.

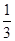 AB,
AB, ABCD的面积是2,AB=a,BC=b,点E从点A出发沿AB以每秒v个单位长的速度向点B运动,点F从点B出发沿BC以每秒
ABCD的面积是2,AB=a,BC=b,点E从点A出发沿AB以每秒v个单位长的速度向点B运动,点F从点B出发沿BC以每秒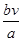 个单位长的速度向点C运动.E、F分别从点A、B同时出发,当其中一点到达端点时,另一点也随之停止运动.请问四边形DEBF的面积的值是否随着时间t的变化而变化?若不变,请写出这个值 ,并写出理由;若变化,说明是怎样变化的.
个单位长的速度向点C运动.E、F分别从点A、B同时出发,当其中一点到达端点时,另一点也随之停止运动.请问四边形DEBF的面积的值是否随着时间t的变化而变化?若不变,请写出这个值 ,并写出理由;若变化,说明是怎样变化的.