题目内容
【题目】材料:在学习绝对值时,老师教过我们绝对值的几何含义,![]() 表示
表示![]() 、
、![]() 在数轴上对应的两点之间的距离;
在数轴上对应的两点之间的距离;![]() ,所以
,所以![]() 表示
表示![]() 、
、![]() 在数轴上对应的两点之间的距离;
在数轴上对应的两点之间的距离;![]() ,所以
,所以![]() 表示
表示![]() 在数轴上对应的点到原点的距离,一般地,点
在数轴上对应的点到原点的距离,一般地,点![]() 、
、![]() 在数轴上分别表示有理数
在数轴上分别表示有理数![]() 、
、![]() ,那么
,那么![]() 、
、![]() 之间的距离可表示为
之间的距离可表示为![]() .
.
(![]() )点
)点![]() 、
、![]() 、
、![]() 在数轴上分别表示有理数
在数轴上分别表示有理数![]() 、
、![]() 、
、![]() ,那么
,那么![]() 到
到![]() 的距离表示为______________________________(用含绝对值的式子表示).如果
的距离表示为______________________________(用含绝对值的式子表示).如果![]() ,那么
,那么![]() 为______________________________.
为______________________________.
(![]() )利用数轴探究:
)利用数轴探究:
①找出满足![]() 的
的![]() 的所有整数值是____________________;
的所有整数值是____________________;
②设![]() ,当
,当![]() 的值取在不小于
的值取在不小于![]() 且不大于
且不大于![]() 的范围时,
的范围时,![]() 的值是不变的,而且是
的值是不变的,而且是![]() 的最小值,这个最小值是____________________;
的最小值,这个最小值是____________________;
(![]() )求
)求![]() 的最小值为____________________,此时
的最小值为____________________,此时![]() 的值为____________________.
的值为____________________.
【答案】(1)|x+2|,-4或0;(2)①-2,4;②2;(3)4,2
【解析】
(1)根据两点间的距离公式,可得答案;
(2)①根据两点间的距离公式,分三种情况分析;
②根据当x的值取在不小于1且不大于3的范围时有最小值,化简即可求出p的值;
(3) |x-3|+|x-2|+|x+1|=(|x-3|+|x+1|)+|x-2|,根据问题(2)中的②可知,要使|x-3|+|x+1|的值最小,x的值只要取-1到3之间(包括-1、3)的任意一个数,要使|x-2|的值最小,x应取2,显然当x=2时能同时满足要求,把x=2代入原式计算即可;
(1)A到B的距离表示为:|x-(-2)|=|x+2|,
|AB|=2即|x+2|=2,∴x=-4或x=0.
(2)①根据绝对值的几何含义可得,|x-3|+|x+1|表示数轴上x与3的距离与x与-1的距离之和,
若x<-1,则3-x+(-x-1)=6,即x=-2;
若-1≤x≤3,则3-x+x+1=6,方程无解,舍去;
若x>3,则x-3+x+1=6,即x=4,
∴满足|x-3|+|x+1|=6的x的所有值是-2,4;
②当x的值取在不小于1且不大于3的范围时,p的值是不变的,而且是p的最小值.
|x3|+|x+1|=3-x+x+3=4,
即p=4,则这个最小值是4;
(3)|x-3|+|x-2|+|x+1|=(|x-3|+|x+1|)+|x-2|,根据问题(2)中的②可知,要使|x-3|+|x+1|的值最小,x的值只要取-1到3之间(包括-1、3)的任意一个数,要使|x-2|的值最小,x应取2,当x=2时能同时满足要求,把x=2代入,原式=1+0+3=4.

 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
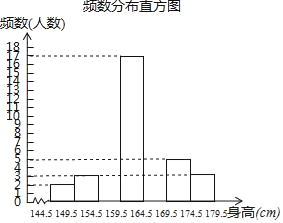
计算高手系列答案【题目】为了解同学们的身体发育情况,学校体卫办公室对七年级全体学生进行了身高测量(精确到1cm),并从中抽取了部分数据进行统计,请根据尚未完成的频数分布表和频数分布直方图解答下列问题:
频率分布表
分组 | 频数 | 百分比 |
144.5~149.5 | 2 | 4% |
149.5~154.5 | 3 | 6% |
154.5~159.5 | a | 16% |
159.5~164.5 | 17 | 34% |
164.5~169.5 | b | n% |
169.5~174.5 | 5 | 10% |
174.5~179.5 | 3 | 6% |
(1)求a、b、n的值;
(2)补全频数分布直方图;
(3)学校准备从七年级学生中选拔护旗手,要求身高不低于170cm,如果七年级有学生350人,护旗手的候选人大概有多少?