题目内容
A，B，C，D，依次是⊙O上的四个点，
，弦AB，CD的延长线交于P点，若∠ABD=60°，则∠P等于
- A.40°
- B.10°
- C.20°
- D.30°
C
分析：根据圆周角的度数等于它所对的弧的度数的一半得到弧AD的度数=2×60°=120°，则弧ABCD的度数=360°-120°=240°，而，则弧BC的度数=
×240°=80°，得到∠BDC=40°，再根据三角形外角性质即可求出∠P．
解答：
解：如图，
∵∠ABD=60°，
∴弧AD的度数=2×60°=120°，
∴弧ABCD的度数=360°-120°=240°，
又∵，
∴弧BC的度数=×240°=80°，
∴∠BDC=40°，
而∠ABD=∠P+∠BDP，
∴∠P=60°-40°=20°．
故选C．
点评：本题考查了在同圆或等圆中，如果两个圆心角以及它们对应的两条弧、两条弦中有一组量相等，则另外两组量也对应相等．也考查了圆周角的度数等于它所对的弧的度数的一半以及三角形外角的性质．
分析：根据圆周角的度数等于它所对的弧的度数的一半得到弧AD的度数=2×60°=120°，则弧ABCD的度数=360°-120°=240°，而
，则弧BC的度数=×240°=80°，得到∠BDC=40°，再根据三角形外角性质即可求出∠P．解答：
解：如图，∵∠ABD=60°，
∴弧AD的度数=2×60°=120°，
∴弧ABCD的度数=360°-120°=240°，
又∵
，∴弧BC的度数=
×240°=80°，∴∠BDC=40°，
而∠ABD=∠P+∠BDP，
∴∠P=60°-40°=20°．
故选C．
点评：本题考查了在同圆或等圆中，如果两个圆心角以及它们对应的两条弧、两条弦中有一组量相等，则另外两组量也对应相等．也考查了圆周角的度数等于它所对的弧的度数的一半以及三角形外角的性质．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
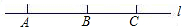如图，如果直线L上依次有3个点A、B、C，那么
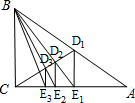如图，已知Rt△ABC，D1是斜边AB的中点，过D1作D1E1⊥AC于E1，连接BE1交CD1于D2；过D2作D2E2⊥AC于E2，连接BE2交CD1于D3；过D3作D3E3⊥AC于E3，…，如此继续，可以依次得到点E4、E5、…、En，分别记△BCE1、△BCE2、△BCE3…△BCEn的面积为S1、S2、S3、…Sn．则Sn=
一个进口时，只有乘积是3的倍数，才可以进入迷宫中心，现让小军从最外环任一个进口进入．