题目内容
 如图所示,点E为正方形ABCD的边CD上的一点,F为边BC的延长线上一点,且CF=CE.若正方形ABCD的边长为2,且CE=x,△DEF的面积为y,请写出y与x之间的函数关系式为________.
如图所示,点E为正方形ABCD的边CD上的一点,F为边BC的延长线上一点,且CF=CE.若正方形ABCD的边长为2,且CE=x,△DEF的面积为y,请写出y与x之间的函数关系式为________.
y=- x2+x
x2+x
分析:由已知可得△DEF的面积= CF•DE,CF=CE=x,DE=CD-CE=2-x,从而得出y与x之间的函数关系式.
CF•DE,CF=CE=x,DE=CD-CE=2-x,从而得出y与x之间的函数关系式.
解答:已知正方形ABCD的边长为2,
∴CD=2,
∵四边形ABCD是正方形,
∴CF=CE=x,
∴△DEF的面积y= CF•DE=
CF•DE= CE•(CD-CE)=
CE•(CD-CE)= x(2-x)=-
x(2-x)=- x2+x.
x2+x.
故答案为:y=- x2+x.
x2+x.
点评:此题考查的知识点是正方形的性质,关键是根据已知和正方形的性质表示出△DEF的面积.
 x2+x
x2+x分析:由已知可得△DEF的面积=
 CF•DE,CF=CE=x,DE=CD-CE=2-x,从而得出y与x之间的函数关系式.
CF•DE,CF=CE=x,DE=CD-CE=2-x,从而得出y与x之间的函数关系式.解答:已知正方形ABCD的边长为2,
∴CD=2,
∵四边形ABCD是正方形,
∴CF=CE=x,
∴△DEF的面积y=
 CF•DE=
CF•DE= CE•(CD-CE)=
CE•(CD-CE)= x(2-x)=-
x(2-x)=- x2+x.
x2+x.故答案为:y=-
 x2+x.
x2+x.点评:此题考查的知识点是正方形的性质,关键是根据已知和正方形的性质表示出△DEF的面积.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目

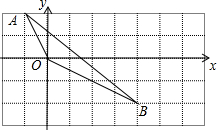 B先沿x轴正方向平移3个单位,再沿y轴负方向平移1个单位得到△A1O1B1.
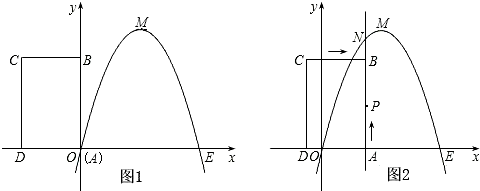
B先沿x轴正方向平移3个单位,再沿y轴负方向平移1个单位得到△A1O1B1. (2012•茂名)如图所示,抛物线y=ax2+
(2012•茂名)如图所示,抛物线y=ax2+ (2013•遵义)我市某中学在创建“特色校园”的活动中,将本校的办学理念做成宣传牌(AB),放置在教学楼的顶部(如图所示).小明在操场上的点D处,用1米高的测角仪CD,从点C测得宣传牌的底部B的仰角为37°,然后向教学楼正方向走了4米到达点F处,又从点E测得宣传牌的顶部A的仰角为45°.已知教学楼高BM=17米,且点A,B,M在同一直线上,求宣传牌AB的高度(结果精确到0.1米,参考数据:
(2013•遵义)我市某中学在创建“特色校园”的活动中,将本校的办学理念做成宣传牌(AB),放置在教学楼的顶部(如图所示).小明在操场上的点D处,用1米高的测角仪CD,从点C测得宣传牌的底部B的仰角为37°,然后向教学楼正方向走了4米到达点F处,又从点E测得宣传牌的顶部A的仰角为45°.已知教学楼高BM=17米,且点A,B,M在同一直线上,求宣传牌AB的高度(结果精确到0.1米,参考数据: