题目内容
 (2013•遵义)我市某中学在创建“特色校园”的活动中,将本校的办学理念做成宣传牌(AB),放置在教学楼的顶部(如图所示).小明在操场上的点D处,用1米高的测角仪CD,从点C测得宣传牌的底部B的仰角为37°,然后向教学楼正方向走了4米到达点F处,又从点E测得宣传牌的顶部A的仰角为45°.已知教学楼高BM=17米,且点A,B,M在同一直线上,求宣传牌AB的高度(结果精确到0.1米,参考数据:
(2013•遵义)我市某中学在创建“特色校园”的活动中,将本校的办学理念做成宣传牌(AB),放置在教学楼的顶部(如图所示).小明在操场上的点D处,用1米高的测角仪CD,从点C测得宣传牌的底部B的仰角为37°,然后向教学楼正方向走了4米到达点F处,又从点E测得宣传牌的顶部A的仰角为45°.已知教学楼高BM=17米,且点A,B,M在同一直线上,求宣传牌AB的高度(结果精确到0.1米,参考数据:| 3 |
分析:首先过点C作CN⊥AM于点N,则点C,E,N在同一直线上,设AB=x米,则AN=x+(17-1)=x+16(米),则在Rt△AEN中,∠AEN=45°,可得EN=AN=x+16,在Rt△BCN中,∠BCN=37°,BM=17,可得tan∠BCN=
=0.75,则可得方程:
=
,解此方程即可求得答案.
| BN |
| CN |
| 17-1 |
| x+20 |
| 3 |
| 4 |
解答: 解:过点C作CN⊥AM于点N,则点C,E,N在同一直线上,
解:过点C作CN⊥AM于点N,则点C,E,N在同一直线上,
设AB=x米,则AN=x+(17-1)=x+16(米),
在Rt△AEN中,∠AEN=45°,
∴EN=AN=x+16,
在Rt△BCN中,∠BCN=37°,BM=17,
∴tan∠BCN=
=0.75,
∴
=
,
解得:x=1
≈1.3.
经检验:x=1
是原分式方程的解.
答:宣传牌AB的高度约为1.3m.
 解:过点C作CN⊥AM于点N,则点C,E,N在同一直线上,
解:过点C作CN⊥AM于点N,则点C,E,N在同一直线上,设AB=x米,则AN=x+(17-1)=x+16(米),
在Rt△AEN中,∠AEN=45°,
∴EN=AN=x+16,
在Rt△BCN中,∠BCN=37°,BM=17,
∴tan∠BCN=
| BN |
| CN |
∴
| 17-1 |
| x+20 |
| 3 |
| 4 |
解得:x=1
| 1 |
| 3 |
经检验:x=1
| 1 |
| 3 |
答:宣传牌AB的高度约为1.3m.
点评:此题考查了仰角的定义.注意能借助仰角构造直角三角形并解直角三角形是解此题的关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
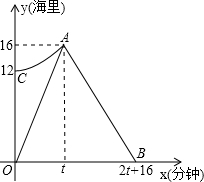 (2013•连云港)我市某海域内有一艘轮船发生故障,海事救援船接到求救信号后立即从港口出发沿直线匀速前往救援,与故障渔船会合后立即将其拖回.如图折线段O-A-B表示救援船在整个航行过程中离港口的距离y(海里)随航行时间x(分钟)的变化规律.抛物线y=ax2+k表示故障渔船在漂移过程中离港口的距离y(海里)随漂移时间x(分钟)的变化规律.已知救援船返程速度是前往速度的
(2013•连云港)我市某海域内有一艘轮船发生故障,海事救援船接到求救信号后立即从港口出发沿直线匀速前往救援,与故障渔船会合后立即将其拖回.如图折线段O-A-B表示救援船在整个航行过程中离港口的距离y(海里)随航行时间x(分钟)的变化规律.抛物线y=ax2+k表示故障渔船在漂移过程中离港口的距离y(海里)随漂移时间x(分钟)的变化规律.已知救援船返程速度是前往速度的