题目内容
【题目】直线y=﹣![]() x+
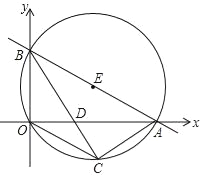
x+![]() 分别与x轴、y轴交于A、B两点,⊙E经过原点O及A、B两点,C是⊙E上一点,连接BC交OA于点D,∠COD=∠CBO.
分别与x轴、y轴交于A、B两点,⊙E经过原点O及A、B两点,C是⊙E上一点,连接BC交OA于点D,∠COD=∠CBO.
(1)求A、B、C三点坐标;
(2)求经过O、C、A三点的抛物线解析式;
(3)直线AB上是否存在点P,使得△COP的周长最小?若存在,请求出P点坐标;若不存在,请说明理由.
【答案】(1)点A(3,0),点B(0,![]() ),点C(
),点C(![]() ,
,![]() );(2)y=
);(2)y=![]() x2﹣
x2﹣![]() x;(3)点P的坐标为(
x;(3)点P的坐标为(![]() ,
,![]() ).
).
【解析】分析:(1)由直线y=-![]() x+
x+![]() 分别与x轴、y轴交于A、B两点,即可求得点A与点B的坐标,然后连接EC,交x轴于点H,由∠COD=∠CBO,根据垂径定理的即可求得OH与AH的长,由勾股定理,可求得AB的长,EH的长,继而求得点C的坐标;
分别与x轴、y轴交于A、B两点,即可求得点A与点B的坐标,然后连接EC,交x轴于点H,由∠COD=∠CBO,根据垂径定理的即可求得OH与AH的长,由勾股定理,可求得AB的长,EH的长,继而求得点C的坐标;
(2)利用待定系数法即可求得经过O、C、A三点的抛物线解析式;
(3)由OC已知,可得当OP+CP最小时,△COP的周长最小;过点O作OF⊥AB于点F,并延长交⊙O于点K,连接CK交直线AB于点P,此点即为所求;易证得CK是直径,则可得点P与点E重合,继而求得P点坐标.
详解:(1)∵直线y=﹣![]() x+
x+![]() 分别与x轴、y轴交于A、B两点,
分别与x轴、y轴交于A、B两点,
∴当x=0时,y=![]() ,当y=0时,x=3,
,当y=0时,x=3,
∴点A(3,0),点B(0,![]() )
)
∴AB=![]() =2
=2![]() ,
,
∴AE=BE=![]() AB=
AB=![]() ,
,
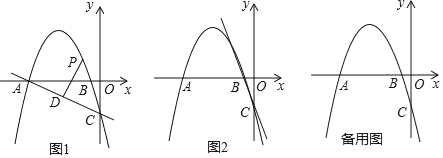
如图1,连接EC,交x轴于点H,
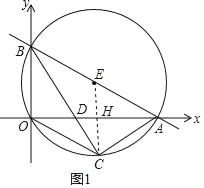
∵∠COD=∠CBO,
∴![]() ,
,
∴EC⊥OA,OC=AC,
∴OH=AH=![]() OA=
OA=![]() ,
,
在Rt△AEH中,EH=![]()
![]() ,
,
∴CH=EC﹣EH=![]() ,
,
∴点C的坐标为(![]() ,﹣
,﹣![]() );
);
(2)设经过O、C、A三点的抛物线的解析式为y=ax(x﹣3),
∵点C的坐标为(![]() ,﹣
,﹣![]() );
);
∴﹣![]() =a×
=a×![]() ×(
×(![]() ﹣3),
﹣3),
解得:a=![]() ,
,
∴经过O、C、A三点的抛物线的解析式为:y=![]() x2﹣
x2﹣![]() x;
x;
(3)存在.
∵OC=![]() ,
,
∴当OP+CP最小时,△COP的周长最小,
如图2,过点O作OF⊥AB于点F,并延长交⊙O于点K,连接CK交直线AB于点P,此点P即为所求;
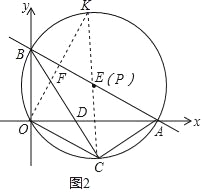
∵∠OAB=30°,
∴∠AOF=60°,
∵∠COD=30°,
∴∠COK=90°,
∴CK是直径,
∵点P在直线AB上,
∴点P与点E重合;
∵点E的横坐标为:![]() ,
,
∴y=﹣![]() ×
×![]() +
+![]() =
=![]() ,
,
∴点P的坐标为(![]() ,
,![]() ).
).

 心算口算巧算一课一练系列答案
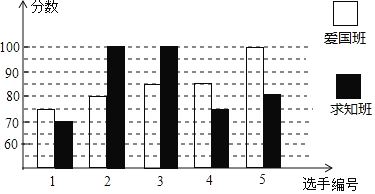
心算口算巧算一课一练系列答案【题目】某校初二开展英语拼写大赛,爱国班和求知班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩如图所示:
(1)根据图示填写下表:
班级 | 中位数(分) | 众数(分) | 平均数(分) |
爱国班 | 85 | ||
求知班 | 100 | 85 |
(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩比较好?
(3)已知爱国班复赛成绩的方差是70,请求出求知班复赛成绩的方差,并说明哪个班成绩比较稳定?