题目内容
如图所示，以点O为圆心的两个同心圆中，大圆的弦AB是小圆的切线，点P为切点，且AB=4，OP=2，连接OA交小圆于点E，则扇形EOP的面积为 ．
【答案】分析：已知大圆的弦AB是小圆的切线，则OP垂直并且平分弦AB，AP=2，△OAP为等腰直角三角形，那么∠AOP=45°，代入扇形面积公式即可．
解答：解：由题意得，AP=PB=
AB=2，
∴可得∠AOP=45°，
∴SOEP=
=
π．
故答案为：
π．
点评：本题考查了扇形面积的计算、垂径定理，解答本题的关键是确定∠AOP=45°，难度一般，注意各知识点的融会贯通．
解答：解：由题意得，AP=PB=
AB=2，∴可得∠AOP=45°，
∴SOEP=
=π．故答案为：
π．点评：本题考查了扇形面积的计算、垂径定理，解答本题的关键是确定∠AOP=45°，难度一般，注意各知识点的融会贯通．
练习册系列答案
阅读快车系列答案
相关题目
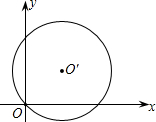如图所示，以点O′（1，1）为圆心，OO′为半径画圆．判断点Q（1，0），点R（2，2）和⊙O′的位置关系．
如图所示，以点O为圆心的两个同心圆中，大圆的弦AB是小圆的切线，点P为切点，且AB=4，OP=2，连接OA交小圆于点E，则扇形EOP的面积为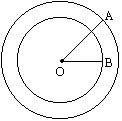
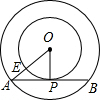如图所示，以点O为圆心的两个同心圆中，大圆的弦AB是小圆的切线，点P为切点，且AB=4，OP=2，连接OA交小圆于点E，则扇形EOP的面积为________．