题目内容
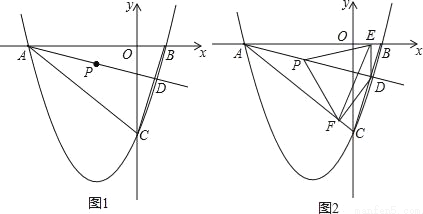
如图1,二次函数y=ax2+bx+c的图象与x轴分别交于A、B两点,与y轴交于点C.若tan∠ABC=3,一元二次方程ax2+bx+c=0的两根为﹣8、2.
(1)求二次函数的解析式;
(2)直线l绕点A以AB为起始位置顺时针旋转到AC位置停止,l与线段BC交于点D,P是AD的中点.
①求点P的运动路程;
②如图2,过点D作DE垂直x轴于点E,作DF⊥AC所在直线于点F,连结PE、PF,在l运动过程中,∠EPF的大小是否改变?请说明理由;
(3)在(2)的条件下,连结EF,求△PEF周长的最小值.
练习册系列答案
相关题目


 ;
; ;
;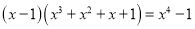 ;
;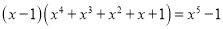 .
. ________;
________;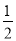 ×99
×99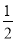 .
.
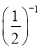 ﹣
﹣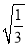 ×
×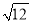 ;
;  .
.
 B. 6 C. 3
B. 6 C. 3
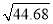 的值为(结果精确到0.01位)( )
的值为(结果精确到0.01位)( )