题目内容
反比例函数y=
与一次函数y=kx+m的图象有一个交点是（-2，1），求它们的另一个交点的坐标，
【答案】分析：先将点（-2，1）代入反比例函数中，求得k的值，再代入一次函数中求得m的值，将两个方程联立起来即可求得另一个交点坐标．
解答：解：将点（-2，1）代入反比例函数y=
中，
得k=-2，
再将点（-2，1）代入一次函数y=kx+m中，
得m=-3
联立两个方程
，
解得另一个交点的坐标为（
，-4）．
点评：本题考查待定系数法求反比例函数和一次函数的解析式后再求交点坐标，比较简单，要熟练掌握．
解答：解：将点（-2，1）代入反比例函数y=
中，得k=-2，
再将点（-2，1）代入一次函数y=kx+m中，
得m=-3
联立两个方程
，解得另一个交点的坐标为（
，-4）．点评：本题考查待定系数法求反比例函数和一次函数的解析式后再求交点坐标，比较简单，要熟练掌握．
练习册系列答案
相关题目
某商店在1-10月份的时间销售A、B两种电子产品，已知产品A每个月的售价y（元）与月份x（1≤x≤10，且x为整数）之间的关系可用如下表格表示：
已知产品A的进价为140元/件，A产品的销量z（件）与月份x的关系式为z=20x；已知B产品的进价为450元/件，产品B的售价m（元）与月份x（1≤x≤10，且x为整数）之间的函数关系式为m=-20x+750，产品B的销量p（件）与月份x的关系可用如下的图象反映．
已知该商店每个月需固定支出500元的物管杂费以及5个员工的工资，已知员工每人每月的工资为1500元．请结合上述信息解答下列问题：
（1）请观察表格与图象，用我们所学习的一次函数，反比例函数，或者二次函数写出y与x的函数关系式，p与x的函数关系式；
（2）试表示出商店每月销售A、B两种产品的总利润W（将每月必要的开支除去）与月份x的函数关系式，并求出该商店在哪个月时获得最大利润；
（3）为了鼓励员工的积极性，在最后4个月的销售期间商店老板决定奖励员工，除了正常的工资外，每卖一件A产品，每个员工都提成0.75元，每卖一件B产品每个员工都提成10元，这样A产品的销量将每月减少12x件，而B产品的销量将每月增加15x件；请问在第几月时总利润（除去当月所有支出部分）可达到16750元？
（参考数据：
=22.47，
=4.583）
| 时间x（月） | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 售价y（元） | 720 | 360 | 240 | 180 | 144 | 120 | 120 | 120 | 120 | 120 |
已知该商店每个月需固定支出500元的物管杂费以及5个员工的工资，已知员工每人每月的工资为1500元．请结合上述信息解答下列问题：
（1）请观察表格与图象，用我们所学习的一次函数，反比例函数，或者二次函数写出y与x的函数关系式，p与x的函数关系式；
（2）试表示出商店每月销售A、B两种产品的总利润W（将每月必要的开支除去）与月份x的函数关系式，并求出该商店在哪个月时获得最大利润；
（3）为了鼓励员工的积极性，在最后4个月的销售期间商店老板决定奖励员工，除了正常的工资外，每卖一件A产品，每个员工都提成0.75元，每卖一件B产品每个员工都提成10元，这样A产品的销量将每月减少12x件，而B产品的销量将每月增加15x件；请问在第几月时总利润（除去当月所有支出部分）可达到16750元？
（参考数据：
| 505 |
| 21 |
当梯形上、下底之和一定时，梯形的面积与梯形的高的函数关系是（ ）
| A、正比例函数 | B、反比例函数 | C、二次函数 | D、都不是 |
如图，反比例函数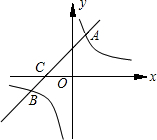
次函数y=mx+b的图象与x轴交于点C．