题目内容
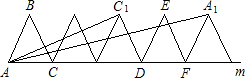 如图,已知边长为2的正三角形ABC沿直线m滚动,当△ABC滚动一周时,到△DEF位置.设△ABC滚动240°时,点C的位置为C1,△ABC滚动480°时,点A的位置为点A1.根据三角函数正切的两角和公式
如图,已知边长为2的正三角形ABC沿直线m滚动,当△ABC滚动一周时,到△DEF位置.设△ABC滚动240°时,点C的位置为C1,△ABC滚动480°时,点A的位置为点A1.根据三角函数正切的两角和公式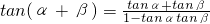 ,∠CAC1+∠CAA1的度数是________°.
,∠CAC1+∠CAA1的度数是________°.
30
分析:过点C1作C1H⊥AF,利用锐角三角函数的定义得出C1H的值及MH的值,再利用三角函数的定义求出tan∠CAC1与tan∠CAA1的值,然后通过等量代换求出∠CAC1+∠CAA1的度数.
解答: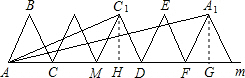 解:设△ABC滚动240°时,C点的位置为C1,△ABC滚动480°时,A点的位置为A1.
解:设△ABC滚动240°时,C点的位置为C1,△ABC滚动480°时,A点的位置为A1.
∵正△ABC的边长为2,
∴C1H=MC1×tan60°=2× =
= 即正△ABC的高为
即正△ABC的高为 ,
,
MH= MD=
MD= ×2=1,
×2=1,
∴tan∠CAC1= =
=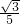 ,
,
tan∠CAA1= =
= ,
,
∴由公式tan(α+β)=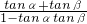 ,
,
得:tan(∠CAC1+∠CAA1),
=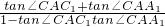 ,
,
=(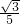 +
+ )÷(1-
)÷(1-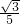 ×
× )
)
= .
.
∴∠CAC1+∠CAA1=30°.
故答案为30°.
点评:本题考查了解直角三角形,等边三角形的性质,旋转的性质,正确判断△ABC滚动的轨迹,利用转化思想和等量代换思想是解答此题的关键.
分析:过点C1作C1H⊥AF,利用锐角三角函数的定义得出C1H的值及MH的值,再利用三角函数的定义求出tan∠CAC1与tan∠CAA1的值,然后通过等量代换求出∠CAC1+∠CAA1的度数.
解答:
 解:设△ABC滚动240°时,C点的位置为C1,△ABC滚动480°时,A点的位置为A1.
解:设△ABC滚动240°时,C点的位置为C1,△ABC滚动480°时,A点的位置为A1.∵正△ABC的边长为2,
∴C1H=MC1×tan60°=2×
 =
= 即正△ABC的高为
即正△ABC的高为 ,
,MH=
 MD=
MD= ×2=1,
×2=1,∴tan∠CAC1=
 =
=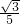 ,
,tan∠CAA1=
 =
= ,
,∴由公式tan(α+β)=
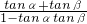 ,
,得:tan(∠CAC1+∠CAA1),
=
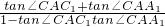 ,
,=(
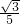 +
+ )÷(1-
)÷(1-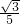 ×
× )
)=
 .
.∴∠CAC1+∠CAA1=30°.
故答案为30°.
点评:本题考查了解直角三角形,等边三角形的性质,旋转的性质,正确判断△ABC滚动的轨迹,利用转化思想和等量代换思想是解答此题的关键.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
 如图,已知边长为4的正方形ABCD中,E为AD中点,P为CE中点,F为BP中点,FH⊥BC交BC于H,连接PH,则下列结论正确的是( )
如图,已知边长为4的正方形ABCD中,E为AD中点,P为CE中点,F为BP中点,FH⊥BC交BC于H,连接PH,则下列结论正确的是( )①BE=CE;②sin∠EBP=
| 1 |
| 2 |
| A、①④⑤ | B、①②③ |
| C、①②④ | D、①③④ |
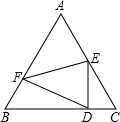 如图,已知边长为5的等边三角形ABC纸片,点E在AC边上,点F在AB边上,沿着EF折叠,使点A落在BC边上的点D的位置,且ED⊥BC,则CE的长是( )
如图,已知边长为5的等边三角形ABC纸片,点E在AC边上,点F在AB边上,沿着EF折叠,使点A落在BC边上的点D的位置,且ED⊥BC,则CE的长是( )A、10
| ||
B、10-5
| ||
C、5
| ||
D、20-10
|
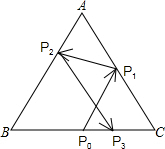 如图,已知边长为2的正三角形ABC中,P0是BC边的中点,一束光线自P0发出射到AC上的点P1后,依次反射到AB、BC上的点P2和P3(反射角等于入射角),且1<BP3<
如图,已知边长为2的正三角形ABC中,P0是BC边的中点,一束光线自P0发出射到AC上的点P1后,依次反射到AB、BC上的点P2和P3(反射角等于入射角),且1<BP3<| 3 |
| 2 |
A、1<P1C<
| ||||
B、
| ||||
C、
| ||||
D、
|
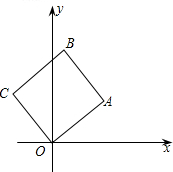 如图,已知边长为l的正方形OABC在直角坐标系中,A、B两点在第一象限内,OA与x轴的夹角为30°,那么点B的坐标是
如图,已知边长为l的正方形OABC在直角坐标系中,A、B两点在第一象限内,OA与x轴的夹角为30°,那么点B的坐标是 用三角函数中正切的两角和公式:tan(α+β)=(tanα+tanβ)÷(1-tanα•tanβ),求出∠CAC′+∠CAA′的度数.( )
用三角函数中正切的两角和公式:tan(α+β)=(tanα+tanβ)÷(1-tanα•tanβ),求出∠CAC′+∠CAA′的度数.( )