题目内容
【题目】如图1,点![]() 点
点![]() 的坐标分别为
的坐标分别为![]() ,且
,且![]() 将线段
将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到线段
得到线段![]() .
.
(1)直接写出![]() __,
__,![]() __ _,点
__ _,点![]() 的坐标为 _;
的坐标为 _;
(2)如图2,作![]() 轴于点
轴于点![]() 点
点![]() 是
是![]() 的中点,点
的中点,点![]() 在
在![]() 内部,
内部,![]() 求证:
求证:![]()
(3)如图3,点![]() 是第二象限内的一个动点,若
是第二象限内的一个动点,若![]() 求线段
求线段![]() 的最大值.
的最大值.

【答案】(1)![]() ,
,![]() ,(4,3) (2)见解析 (3)
,(4,3) (2)见解析 (3)![]()
【解析】
(1)由非负性可求![]() ,
,![]() 的值,过点
的值,过点![]() 作
作![]() 于
于![]() ,由“
,由“![]() ”可证
”可证![]() ,可得
,可得![]() ,
,![]() ,可求点
,可求点![]() 坐标;
坐标;
(2)连接![]() ,作
,作![]() 交
交![]() 于
于![]() ,由“
,由“![]() ”可证
”可证![]() ,可得
,可得![]() ,
,![]() ,即可得结论;
,即可得结论;
(3)取![]() 中点
中点![]() ,连接
,连接![]() ,
,![]() ,由三角形三边关系可得
,由三角形三边关系可得![]() ,则当点
,则当点![]() 在
在![]() 上时,
上时,![]() 有最大值为
有最大值为![]() .
.
解:(1)![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() 点
点![]() ,点
,点![]() ,
,
如图,过点![]() 作
作![]() 于
于![]() ,
,
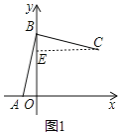
![]() 将线段
将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到线段
得到线段![]() .
.
![]() ,
,![]() ,
,
![]() ,且
,且![]() ,
,
![]() ,且
,且![]() ,
,![]() ,
,
![]()
![]() ,
,![]() ,
,
![]() ,
,
![]() 点
点![]()
故答案为:![]() ,4,
,4,![]()
(2)连接![]() ,作
,作![]() 交
交![]() 于
于![]() ,
,
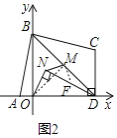
![]() 轴,
轴,
![]() ,
,
![]() ,
,
![]() 点
点![]() 是
是![]() 的中点,
的中点,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,且
,且![]() ,
,![]() ,
,
![]()
![]() ,
,![]() ,
,
![]() ,
,
![]()
![]() ;
;
(3)如图3,点P在以OB为直径的圆上,取![]() 中点
中点![]() ,连接
,连接![]() ,
,![]() ,
,
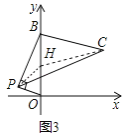
![]() ,点
,点![]() 是
是![]() 中点,
中点,![]() ,
,
![]() ,
,
![]() 点
点![]() ,点
,点![]() ,
,
![]() ,
,
![]() ,
,
![]() 当点
当点![]() 在
在![]() 上时,
上时,![]() 有最大值为
有最大值为![]() .
.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
【题目】2020年2月初,在抵御新冠肺炎的工作中,全国各地口罩严重供应不足,某乡镇企业缝纫车间立即转岗做口罩以供应本地志愿者和卫生系统,该车间有技术工人15人,生产部为了合理制定口罩的日生产定额,统计了15人某天加工口罩数如下:
车间15名工人某一天加工口罩个数统计表
加工零件数/个 | 540 | 450 | 300 | 240 | 210 | 120 |
人数 | 1 | 1 | 2 | 6 | 3 | 2 |
(1)求这一天15名工人加工口罩数的平均数、中位数和众数.
(2)为了提高大多数工人的积极性,管理者准备试行“每天定额生产,超产有奖”的措施,假如你是管理者,从平均数、中位数、众数的角度进行分析,你将如何确定这个“定额”?