题目内容
20、如图，在以点O为圆心的两个圆中，大圆的弦AB交小圆于点C、D，求证：AC=BD．分析：过圆心O作OE⊥AB于点E，根据垂径定理得到AE=BE，同理得到CE=DE，又因为AE-CE=BE-DE，进而求证出AC=BD．
解答：
证明：过圆心O作OE⊥AB于点E，
在大圆O中，OE⊥AB，
∴AE=BE．
在小圆O中，OE⊥CD，
∴CE=DE．
∴AE-CE=BE-DE．
∴AC=BD．
证明：过圆心O作OE⊥AB于点E，在大圆O中，OE⊥AB，
∴AE=BE．
在小圆O中，OE⊥CD，
∴CE=DE．
∴AE-CE=BE-DE．
∴AC=BD．
点评：本题就是考查垂径定理的实际应用．
练习册系列答案
53随堂测系列答案
相关题目
23、如图，在以点O为圆心的两个同心圆中，小圆直径AE的延长线与大圆交于点B，点D在大圆上，BD与小圆相切于点F，AF的延长线与大圆相交于点C，且CE⊥BD．找出图中相等的线段并证明．
22、如图，在以点O为圆心的两个同心圆中，AB经过圆心O，且与小圆相交于A，与大圆相交于点B，小圆的切线AC与大圆相交于D，OC平分∠ACB．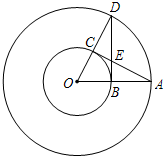
（2006•上海模拟）已知：如图，在以点O为圆心的两个同心圆中，大圆的半径OA与小圆相交于点B，AC与小圆相切于点C，OC的延长线与大圆相交于点D，AC与BD相交于点E．