题目内容
 22、如图,在以点O为圆心的两个同心圆中,AB经过圆心O,且与小圆相交于A,与大圆相交于点B,小圆的切线AC与大圆相交于D,OC平分∠ACB.
22、如图,在以点O为圆心的两个同心圆中,AB经过圆心O,且与小圆相交于A,与大圆相交于点B,小圆的切线AC与大圆相交于D,OC平分∠ACB.(1)证明直线BC是小圆的切线;
(2)试证明:AC+AD=BC;
(3)若AB=8cm,BC=10cm,求大圆与小圆形成的圆环的面积.
分析:(1)作OE⊥BC于E,可证OE=OA,
(2)连接OD,由(1)知AC=CE,再证△AOD≌△EOB,得AD=BE,
(3)由(2)可得BE=4,S圆环=S大圆-S小圆.
(2)连接OD,由(1)知AC=CE,再证△AOD≌△EOB,得AD=BE,
(3)由(2)可得BE=4,S圆环=S大圆-S小圆.
解答:证明:(1)作OE⊥BC于E;
∵CO=CO,∠ACO=∠ECO,∠CAO=∠OEC,
∴△OAC≌△OEC,
∴OE=OA,∴BC是小圆的切线.
(2)连接OD,
在直角三角形AOD与直角三角形EOB中,
∵OD=OB,OA=OE,
∴Rt△AOD≌Rt△EOB,得AD=BE,
∴BC=AD+AC.
(3)由(2)可得BE=4,S圆环=S大圆-S小圆
=π(OB2-OE2)
=π•BE2=16π(cm2).
∵CO=CO,∠ACO=∠ECO,∠CAO=∠OEC,
∴△OAC≌△OEC,
∴OE=OA,∴BC是小圆的切线.
(2)连接OD,

在直角三角形AOD与直角三角形EOB中,
∵OD=OB,OA=OE,
∴Rt△AOD≌Rt△EOB,得AD=BE,
∴BC=AD+AC.
(3)由(2)可得BE=4,S圆环=S大圆-S小圆
=π(OB2-OE2)
=π•BE2=16π(cm2).
点评:本题考查了切线的判定,全等三角形的判定等知识点.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
 23、如图,在以点O为圆心的两个同心圆中,小圆直径AE的延长线与大圆交于点B,点D在大圆上,BD与小圆相切于点F,AF的延长线与大圆相交于点C,且CE⊥BD.找出图中相等的线段并证明.
23、如图,在以点O为圆心的两个同心圆中,小圆直径AE的延长线与大圆交于点B,点D在大圆上,BD与小圆相切于点F,AF的延长线与大圆相交于点C,且CE⊥BD.找出图中相等的线段并证明. 20、如图,在以点O为圆心的两个圆中,大圆的弦AB交小圆于点C、D,求证:AC=BD.
20、如图,在以点O为圆心的两个圆中,大圆的弦AB交小圆于点C、D,求证:AC=BD.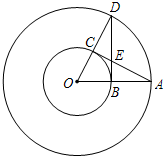 (2006•上海模拟)已知:如图,在以点O为圆心的两个同心圆中,大圆的半径OA与小圆相交于点B,AC与小圆相切于点C,OC的延长线与大圆相交于点D,AC与BD相交于点E.
(2006•上海模拟)已知:如图,在以点O为圆心的两个同心圆中,大圆的半径OA与小圆相交于点B,AC与小圆相切于点C,OC的延长线与大圆相交于点D,AC与BD相交于点E.