Question

如图，抛物线y＝ax²－2ax－3a(a＜0)，与x轴的交于A、B两点(点A在点B的右侧)，与y轴的正半轴交于点C，顶点为D

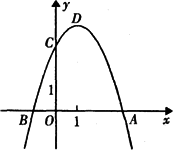
(1)求顶点D的坐标(用含a的代数式表示)；

(2)若以AD为直径的圆经过点C、①求抛物线的解析式；

②如图，点E是y轴负半轴上的一点，连结BE，将△OBE绕平面内某一点旋转180°，得到△PMN(点P、M、N分别和点O、B、E对应)，并且点M、N都在抛物线上，作MF⊥x轴于点F，若线段MF：BF＝1：2，求点M、N的坐标；

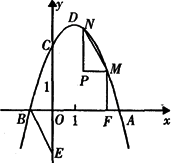
③点Q在抛物线的对称轴上，以Q为圆心的圆过A、B两点，并且和直线CD相切，如图，求点Q的坐标．

Answer 1

答案：
解析：

解：(1) 　　∴　2分 　　(2)①令，则 　　∵点A在点B的右侧 　　∴ 　　令，则 　　∴ 作于点E 　　∵AD是直径 　　∴∠ACD＝90°∴∠OCA＋∠ECD＝90° 　　又∵∠EDC＋∠ECD＝90° 　　∴∠EDC＝∠OCA， 　　又∵∠DEC＝∠COA＝90°∴△DEC∽△COA 　　∴即　a2＝1 　　∵　 ∴a＝－1 　　∴　5分 　　②∵△OBE绕平面内某一点旋转180°得到△PMN， 　　且△OBE是直角三角形 　　∴PM∥，PN∥ 　　设 　　则， 　　∵MF：BF＝1：2 　　∴　 　　∴　8分 　　∵旋转，∴， 　　∴， 　　∴　10分 　　③∵在对称轴上，设， 　　对称轴与轴交于点，圆半径为 　　∵△CDE中，∠DEC＝90°，DE＝CE＝1 　　∴△CDE是等腰直角三角形，即∠EDC＝45°， 　　∴∠ODC＝45° 　　设直线CD切圆Q于点H， 　　则△ODH也是等腰直角三角形 　　∴，即 　　在 　　∴ 　　　14分