题目内容
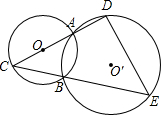如图，⊙O和⊙O′相交于A、B两点，AC是⊙O的直径，如果AC=12，BE=30，BC=AD，则DE=________，∠E=________．
18
30°
分析：根据三角形相似可以得出AD的长度，再结合正弦定理得出∠CAB的度数，即可得出∠E的度数，进而利用余弦定理求出DE的长．
解答：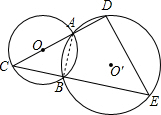
解：连接AB，设AD=x，则BC=x，CD=12+x，CE=30+x
∵△ABC∽△EDC
∴
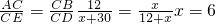
在Rt△ABC中，sin∠CAB=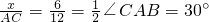
∴∠E=30°，∠C=60°
在△DCE中，DE=12+x=18，CE=x+30=36，
由余弦定理，得DE=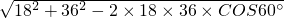
=18，
故答案为：18，30°．
点评：此题主要考查了相似三角形的判定以及余弦定理的应用和正弦定理，题目综合性较强，考查知识比较全面．
30°分析：根据三角形相似可以得出AD的长度，再结合正弦定理得出∠CAB的度数，即可得出∠E的度数，进而利用余弦定理求出DE的长．
解答：
解：连接AB，设AD=x，则BC=x，CD=12+x，CE=30+x∵△ABC∽△EDC
∴
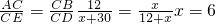
在Rt△ABC中，sin∠CAB=
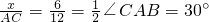
∴∠E=30°，∠C=60°
在△DCE中，DE=12+x=18，CE=x+30=36，
由余弦定理，得DE=
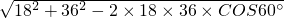=18，故答案为：18
，30°．点评：此题主要考查了相似三角形的判定以及余弦定理的应用和正弦定理，题目综合性较强，考查知识比较全面．
练习册系列答案
相关题目
如图，A和B两个小机器人，自甲处同时出发相背而行，绕直径为整数米的圆周上运动，15分钟内相遇7次，如果A的速度每分钟增加6米，则A和B在15分钟内相遇9次，问圆周直径至多是多少米？至少是多少米？（取π=3.14）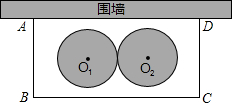
某学校要在围墙旁建一个长方形的中药材种植实习苗圃，苗圃的一边靠围墙（墙的长度不限），另三边用木栏围成，建成的苗圃为如图所示的长方形ABCD．已知木栏总长为120米，设AB边的长为x米，长方形ABCD的面积为S平方米．
和
，且
和
，且