题目内容
(2012•赤峰)如图,直线l1:y=x与双曲线y=
相交于点A(a,2),将直线l1向上平移3个单 位得到l2,直线l2与双曲线相交于B、C两点(点B在第一象限),交y轴于D点.
位得到l2,直线l2与双曲线相交于B、C两点(点B在第一象限),交y轴于D点.
(1)求双曲线y=
的解析式;
(2)求tan∠DOB的值.
| k |
| x |
 位得到l2,直线l2与双曲线相交于B、C两点(点B在第一象限),交y轴于D点.
位得到l2,直线l2与双曲线相交于B、C两点(点B在第一象限),交y轴于D点.(1)求双曲线y=
| k |
| x |
(2)求tan∠DOB的值.
分析:(1)由点A(a,2)在直线y=x上可知a=2,再代入y=
中求k的值即可;
(2)将l1向上平移了3个单位得到l2的解析式为y=x+3,联立l2与双曲线解析式求交点B坐标,根据B点坐标,利用锐角三角函数定义求解.
| k |
| x |
(2)将l1向上平移了3个单位得到l2的解析式为y=x+3,联立l2与双曲线解析式求交点B坐标,根据B点坐标,利用锐角三角函数定义求解.
解答:解:(1)∵A(a,2)是y=x与y=
的交点,
∴A(2,2),
把A(2,2)代入y=
,得k=4,
∴双曲线的解析式为y=
;
(2)∵将l1向上平移了3个单位得到l2,
∴l2的解析式为y=x+3,
∴解方程组
,
得
,
,
∴B (1,4),
∴tan∠DOB=
.
| k |
| x |
∴A(2,2),
把A(2,2)代入y=
| k |
| x |
∴双曲线的解析式为y=
| 4 |
| x |
(2)∵将l1向上平移了3个单位得到l2,
∴l2的解析式为y=x+3,
∴解方程组
|
得
|
|
∴B (1,4),
∴tan∠DOB=
| 1 |
| 4 |
点评:本题考查了反比例函数与一次函数交点问题,一次函数图象与几何变换,锐角三角函数定义.关键是根据y=x求点的坐标,根据点的坐标及平移规律,求函数解析式,再根据函数解析式求交点坐标.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
 (2012•赤峰)如图所示,在△ABC中,∠ABC=∠ACB.
(2012•赤峰)如图所示,在△ABC中,∠ABC=∠ACB.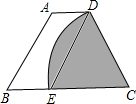 (2012•赤峰)如图,等腰梯形ABCD中,AD∥BC,以点C为圆心,CD为半径的弧与BC交于点E,四边形ABED是平行四边形,AB=3,则扇形CDE(阴影部分)的面积是( )
(2012•赤峰)如图,等腰梯形ABCD中,AD∥BC,以点C为圆心,CD为半径的弧与BC交于点E,四边形ABED是平行四边形,AB=3,则扇形CDE(阴影部分)的面积是( ) (2012•赤峰)如图,在菱形ABCD中,BD为对角线,E、F分别是DC、DB的中点,若EF=6,则菱形ABCD的周长是
(2012•赤峰)如图,在菱形ABCD中,BD为对角线,E、F分别是DC、DB的中点,若EF=6,则菱形ABCD的周长是 (2012•赤峰)如图,王强同学在甲楼楼顶A处测得对面乙楼楼顶D处的仰角为30°,在甲楼楼底B处测得乙楼楼顶D处的仰角为45°,已知甲楼高26米,求乙楼的高度.(
(2012•赤峰)如图,王强同学在甲楼楼顶A处测得对面乙楼楼顶D处的仰角为30°,在甲楼楼底B处测得乙楼楼顶D处的仰角为45°,已知甲楼高26米,求乙楼的高度.( 与点F关于抛物线的对称轴对称,直线AF交y轴于点E,|OC|:|OA|=5:1.
与点F关于抛物线的对称轴对称,直线AF交y轴于点E,|OC|:|OA|=5:1.