题目内容
 (2012•赤峰)如图,王强同学在甲楼楼顶A处测得对面乙楼楼顶D处的仰角为30°,在甲楼楼底B处测得乙楼楼顶D处的仰角为45°,已知甲楼高26米,求乙楼的高度.(
(2012•赤峰)如图,王强同学在甲楼楼顶A处测得对面乙楼楼顶D处的仰角为30°,在甲楼楼底B处测得乙楼楼顶D处的仰角为45°,已知甲楼高26米,求乙楼的高度.(| 3 |
分析:作AE⊥DC于点E,从而判定四边形ABCE是矩形,得到AE=BC AB=EC,设DC=x,在Rt△AED中,利用tan30°=
得到有关x的比例式后即可求得x的值.
| DE |
| AE |
解答:解:作AE⊥DC于点E
∴∠AED=90°
∵∠ABC=∠BCD=∠CEA=90°
∴四边形ABCE是矩形
∴AE=BC AB=EC
设DC=x
∵AB=26
∴DE=x-26
在Rt△AED中,tan30°=
,
即
=
解得:x≈61.1
经检验x≈61.1是原方程的根.
答:乙楼高为61.1米
∴∠AED=90°
∵∠ABC=∠BCD=∠CEA=90°
∴四边形ABCE是矩形

∴AE=BC AB=EC
设DC=x
∵AB=26
∴DE=x-26
在Rt△AED中,tan30°=
| DE |
| AE |
即
| x-26 |
| x |
| ||
| 3 |
解得:x≈61.1
经检验x≈61.1是原方程的根.
答:乙楼高为61.1米
点评:本题考查了解直角三角形的应用,解题的关键是从复杂的实际问题中整理出直角三角形并选择合适的边角关系求解.

练习册系列答案
相关题目
 (2012•赤峰)如图所示,在△ABC中,∠ABC=∠ACB.
(2012•赤峰)如图所示,在△ABC中,∠ABC=∠ACB.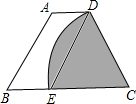 (2012•赤峰)如图,等腰梯形ABCD中,AD∥BC,以点C为圆心,CD为半径的弧与BC交于点E,四边形ABED是平行四边形,AB=3,则扇形CDE(阴影部分)的面积是( )
(2012•赤峰)如图,等腰梯形ABCD中,AD∥BC,以点C为圆心,CD为半径的弧与BC交于点E,四边形ABED是平行四边形,AB=3,则扇形CDE(阴影部分)的面积是( ) (2012•赤峰)如图,在菱形ABCD中,BD为对角线,E、F分别是DC、DB的中点,若EF=6,则菱形ABCD的周长是
(2012•赤峰)如图,在菱形ABCD中,BD为对角线,E、F分别是DC、DB的中点,若EF=6,则菱形ABCD的周长是 与点F关于抛物线的对称轴对称,直线AF交y轴于点E,|OC|:|OA|=5:1.
与点F关于抛物线的对称轴对称,直线AF交y轴于点E,|OC|:|OA|=5:1.