题目内容
已知：如图，AB=AE，BC=ED，AF⊥CD且F是CD的中点，
求证：∠B=∠E．
证明：连接AC，AD，
∵AF⊥CD，F为CD的中点，
∴AC=AD，
在△ABC和△AED中
，
∴△ABC≌△AED，
∴∠B=∠E．
分析：连接AC、AD，根据线段垂直平分线定理求出AC=AD，根据全等三角形的判定SSS证△ABC≌△AED即可．
点评：本题考查了对线段的垂直平分线定理和全等三角形的性质和判定的应用，关键是构造三角形ABC和三角形AED，并推出两三角形全等，题目比较典型，难度适中．
∵AF⊥CD，F为CD的中点，
∴AC=AD，
在△ABC和△AED中
，∴△ABC≌△AED，
∴∠B=∠E．
分析：连接AC、AD，根据线段垂直平分线定理求出AC=AD，根据全等三角形的判定SSS证△ABC≌△AED即可．
点评：本题考查了对线段的垂直平分线定理和全等三角形的性质和判定的应用，关键是构造三角形ABC和三角形AED，并推出两三角形全等，题目比较典型，难度适中．
练习册系列答案
口算能手系列答案
相关题目
8、已知：如图，AB、AC分别切⊙O于B、C，D是⊙O上一点，∠D=40°，则∠A的度数等于（ ）
已知：如图，AB，CD相交于点O，且OA•OD=OB•OC，求证：AC∥DB．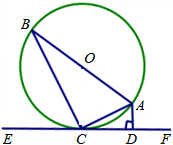
已知：如图，AB是⊙O的直径，AC是弦，直线EF是过点C的⊙O的切线，AD⊥EF于点D．
29、已知，如图，AB∥CD，∠EAB+∠FDC=180°．求证：AE∥FD．
已知：如图，AB=AC，DB=DC，求证：∠B=∠C．