Question

【题目】如图，在正方形中，为的中点，为上的一个动点，若，则的最小值为( )

A. B. C. D.

Answer 1

【答案】D

【解析】

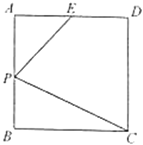
作点C关于AB的对称点F，连接EF，交AB与P，作EH⊥BC，交BC于H，由轴对称的性质可得PF=PC，即可得PE+PC=EF，根据两点之间线段最短可知EF为PE+PF的最小值，由正方形的性质可知EH=AB，BH=AE=AB，利用勾股定理求出EF的长即可.

作点C关于AB的对称点F，连接EF，交AB与P，作EH⊥BC，交BC于H，

∵点C、点F关于AB对称，P在AB上，

∴PF=PC，

∴PE+PC=PE+PF=EF，

∴PE+PF的最小值为EF的长，

∵ABCD为正方形，E是AD中点，

∴EH=AB=2，BH=AE=1，

∴FH=3，

∴EF==.

故选D.