题目内容
在平面直角坐标系中给定以下五个点A(-2,0)、B(1,0)、C(4,0)、D(-2, )、E(0,-6),在五个形状、颜色、质量完全相同的乒乓球上标上A、B、C、D、E代表以上五个点.玩摸球游戏,每次摸三个球,摸一次,三球代表的点恰好能确定一条抛物线(对称轴平行于y轴)的概率是( )
)、E(0,-6),在五个形状、颜色、质量完全相同的乒乓球上标上A、B、C、D、E代表以上五个点.玩摸球游戏,每次摸三个球,摸一次,三球代表的点恰好能确定一条抛物线(对称轴平行于y轴)的概率是( )A.

B.

C.

D.

【答案】分析:写出所有的摸球的可能情况,然后根据函数的定义确定出不能确定抛物线的情况数,再根据概率公式列式计算即可得解.
解答:解:所有的摸球的情况有:(ABC),(ABD),(ABE),(ACD),(ACE),(ADE),(BCD),(BCE),(BDE),(CDE)共10种情况,
其中:ABC时,三点都在x轴上,共线,不能确定一条抛物线,
(ABD),(ACD),(ADE)时,A、D的横坐标都是-2,不符合函数的定义,
所以,能确定一条抛物线的情况数有:10-1-3=6,
所以,P(能确定一条抛物线)= =
= .
.
故选B.
点评:本题是对概率的考查,难点在于根据函数的定义确定出不能确定一条抛物线的情况,还要注意三点共线的情况,是道容易出错的题目.
解答:解:所有的摸球的情况有:(ABC),(ABD),(ABE),(ACD),(ACE),(ADE),(BCD),(BCE),(BDE),(CDE)共10种情况,
其中:ABC时,三点都在x轴上,共线,不能确定一条抛物线,
(ABD),(ACD),(ADE)时,A、D的横坐标都是-2,不符合函数的定义,
所以,能确定一条抛物线的情况数有:10-1-3=6,
所以,P(能确定一条抛物线)=
 =
= .
.故选B.
点评:本题是对概率的考查,难点在于根据函数的定义确定出不能确定一条抛物线的情况,还要注意三点共线的情况,是道容易出错的题目.

练习册系列答案
相关题目

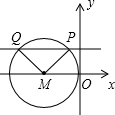 如图,在平面直角坐标系中,⊙M与y轴相切于原点O,平行于x轴的直线交⊙M于P,Q两点,点P在点Q的右方,若点P的坐标是(-1,2),有下列结论:①点Q的坐标是(-4,2);②PQ=3;③△MPQ的面积是3;④M点的坐标是(-3,0).其中正确的结论序号是
如图,在平面直角坐标系中,⊙M与y轴相切于原点O,平行于x轴的直线交⊙M于P,Q两点,点P在点Q的右方,若点P的坐标是(-1,2),有下列结论:①点Q的坐标是(-4,2);②PQ=3;③△MPQ的面积是3;④M点的坐标是(-3,0).其中正确的结论序号是 (2013•安庆二模)在平面直角坐标系中.过一点分別作x轴与y轴的垂线,若与坐标轴围成矩形的周长与面积相等,则这个点叫做和谐点.给出以下结论:①点M(2,4)是和谐点;②不论a为何值时,点P(2,a)不是和谐点;③若点P(a,3)是和谐点,则a=6;④若点F是和谐点,则点F关于坐标轴的对称点也是和谐点.正确结论的序号是
(2013•安庆二模)在平面直角坐标系中.过一点分別作x轴与y轴的垂线,若与坐标轴围成矩形的周长与面积相等,则这个点叫做和谐点.给出以下结论:①点M(2,4)是和谐点;②不论a为何值时,点P(2,a)不是和谐点;③若点P(a,3)是和谐点,则a=6;④若点F是和谐点,则点F关于坐标轴的对称点也是和谐点.正确结论的序号是 (2012•老河口市模拟)如图,在平面直角坐标系中,抛物线y=ax2+bx+c交y轴于A(0,4),交x轴于B、C两点(点B在点C的左侧).B、C两点坐标分别为(3,0),(8,0).
(2012•老河口市模拟)如图,在平面直角坐标系中,抛物线y=ax2+bx+c交y轴于A(0,4),交x轴于B、C两点(点B在点C的左侧).B、C两点坐标分别为(3,0),(8,0).