题目内容
6.(1)分解因式:8(a2+1)-16a;(2)计算:-5x(x2y-xy2)÷y;
(3)计算:$\frac{1-a}{2a-4}÷({a+2+\frac{3}{a-2}})$;
(4)解方程:$\frac{2x+1}{{{x^2}+x}}=\frac{5}{6x+6}$.
分析 (1)首先去括号,进而提取公因式,再利用完全平方公式分解因式得出即可;
(2)首先去括号,进而利用多项式除以单项式运算法则求出即可;
(3)首先将括号里面通分,再利用分式的除法运算法则求出即可;
(4)利用分式方程的解法首先去分母,进而得出即可.
解答 解:(1)8(a2+1)-16a
=8a2+8-16a,
=8(a2-2a+1),
=8(a-1)2;
(2)-5x(x2y-xy2)÷y
=(-5x3y+5x2y2)÷y,
=-5x3+5x2y;
(3)$\frac{1-a}{2a-4}÷({a+2+\frac{3}{a-2}})$
=$\frac{1-a}{2(a-2)}$÷[$\frac{(a+2)(a-2)}{a-2}$+$\frac{3}{a-2}$]
=$\frac{1-a}{2(a-2)}$×$\frac{a-2}{(a-1)(a+1)}$
=-$\frac{1}{2a+2}$;
(4)$\frac{2x+1}{{{x^2}+x}}=\frac{5}{6x+6}$
去分母得:
6×(2x+1)=5x,
解得:$x=-\frac{6}{7}$
经检验$x=-\frac{6}{7}$是原方程的解,故原分式方程的解为:$x=-\frac{6}{7}$.
点评 此题主要考查了分式方程的解法以及分式的混合运算以及整式的混合运算,正确掌握运算法则是解题关键.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
18.下列长度的各种线段,可以组成三角形的是( )
| A. | 1,2,3 | B. | 1,5,5 | C. | 3,3,6 | D. | 3,5,1 |
15.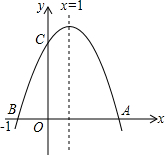 如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,且对称轴为x=1,点B坐标为(-1,0),则下面四个结论:①2a+b=0;②4a-2b+c<0;③ac>0;④当y<0,x<-1或x>2中,正确的序号是( )
如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,且对称轴为x=1,点B坐标为(-1,0),则下面四个结论:①2a+b=0;②4a-2b+c<0;③ac>0;④当y<0,x<-1或x>2中,正确的序号是( )
 如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,且对称轴为x=1,点B坐标为(-1,0),则下面四个结论:①2a+b=0;②4a-2b+c<0;③ac>0;④当y<0,x<-1或x>2中,正确的序号是( )
如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,且对称轴为x=1,点B坐标为(-1,0),则下面四个结论:①2a+b=0;②4a-2b+c<0;③ac>0;④当y<0,x<-1或x>2中,正确的序号是( )| A. | ①③ | B. | ②③ | C. | ①② | D. | ③④ |
16.如果一个三角形的两个内角的差等于第三个内角,你们这个三角形一定是( )
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 无法确定 |
 如图,在平面直角坐标系中,点A(m,2)在第一象限.若点A关于y轴的对称点B在反比例函数$y=-\frac{6}{x}$的图象上,则m的值为( )
如图,在平面直角坐标系中,点A(m,2)在第一象限.若点A关于y轴的对称点B在反比例函数$y=-\frac{6}{x}$的图象上,则m的值为( )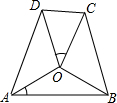 如图,O为四边形ABCD内一点,OA=OB=OC=OD,∠AOB与∠CDO互补,∠OAB与∠COD相等,则$\frac{AB}{CD}$==$\frac{3+\sqrt{5}}{2}$.
如图,O为四边形ABCD内一点,OA=OB=OC=OD,∠AOB与∠CDO互补,∠OAB与∠COD相等,则$\frac{AB}{CD}$==$\frac{3+\sqrt{5}}{2}$. 已知二次函数的图象与x轴的交点坐标为(3,0)和(-1,0),且经过点(1,-4),
已知二次函数的图象与x轴的交点坐标为(3,0)和(-1,0),且经过点(1,-4),