题目内容
已知一次函数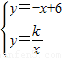 和反比例函数y=
和反比例函数y=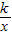 的图象过点A,B,A点横坐标为x1,B点横坐标为x2,且2x2-x1=6,如图所示.
的图象过点A,B,A点横坐标为x1,B点横坐标为x2,且2x2-x1=6,如图所示.(1)求k的值;(2)求△OAB的面积.
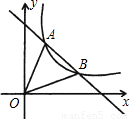
【答案】分析:(1)把两个函数组成方程组,化简成含x的一元二次方程,利用根与系数的关系求解;
(2)△OAB的面积应等于最大三角形的面积减去周围两个三角形的面积.
解答:解:(1) 化简得:x2-6x+k=0,
化简得:x2-6x+k=0,
∴x1+x2=6
∵2x2-x1=6,
∴x2=4,x1=2
当x=4时,y=2,当x=2时,y=4
∴k=2×4=8;
(2)设直线与x轴,y轴分别交于点C,D,
∴C(6,0),D(0,6)
∴△AOB的面积= ×6×6-
×6×6- ×6×2-
×6×2- ×6×2=6.
×6×2=6.
点评:两个函数的交点坐标即为这两个函数解析式组成的方程组的解.注意利用根与系数的关系求解.
(2)△OAB的面积应等于最大三角形的面积减去周围两个三角形的面积.
解答:解:(1)
 化简得:x2-6x+k=0,
化简得:x2-6x+k=0,∴x1+x2=6
∵2x2-x1=6,
∴x2=4,x1=2
当x=4时,y=2,当x=2时,y=4
∴k=2×4=8;
(2)设直线与x轴,y轴分别交于点C,D,
∴C(6,0),D(0,6)
∴△AOB的面积=
 ×6×6-
×6×6- ×6×2-
×6×2- ×6×2=6.
×6×2=6.点评:两个函数的交点坐标即为这两个函数解析式组成的方程组的解.注意利用根与系数的关系求解.

练习册系列答案
相关题目
 和反比例函数
和反比例函数 的图象在平面直角坐标系中交于A、B两点,当y1>y2时,x的取值范围是【 】
的图象在平面直角坐标系中交于A、B两点,当y1>y2时,x的取值范围是【 】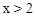 (B)
(B)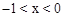 (C)
(C)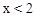 ,
,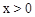

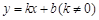 和反比例函数
和反比例函数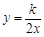 的图象交于点A(1,1).
的图象交于点A(1,1).
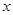 轴上一点,且△AOB是直角三角形,求B点的坐标.
轴上一点,且△AOB是直角三角形,求B点的坐标.