Question

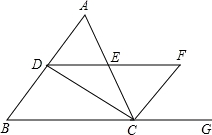
如图，在△ABC中，CD与CF分别是△ABC的内角、外角平分线，DF∥BC交AC于点E．试说明：

（1）△DCF为直角三角形；

（2）DE=EF．

Answer 1

【考点】等腰三角形的判定与性质；平行线的性质．

【专题】证明题．

【分析】（1）根据角平分线定义得出∠DCE=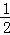∠ACB，∠ECF=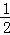∠ACG，从而得出∠DCF=90°；

（2）再由平行线的性质得出∠EDC=∠BCD，即可得ED=EC．

【解答】证明：（1）∵CD与CF分别是△ABC的内角、外角平分线，

∴∠DCE=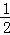∠ACB，∠ECF=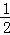∠ACG，

∵∠ACB+∠ACG=180°，

∴∠DCE+∠ECF=90°，

∴△DCF为直角三角形；

（2）∵DF∥BC，

∴∠EDC=∠BCD，

∵∠ECD=∠BCD，

∴∠EDC=∠ECD，

∴ED=EC，

同理，EF=EC，

∴DE=EF．

【点评】本题考查了等腰三角形的判定和性质以及平行线的性质，是基础知识比较简单．